Skip to contents

Multi Value Trait Analysis with `pcvr`

pcvr v1.0.0

Josh Sumner

Source: vignettes/articles/pcvrTutorial_mvt.Rmd
pcvrTutorial_mvt.Rmd

Outline

  • pcvr Goals
  • Load Package
  • What are multi value traits?
  • Multi value trait format
  • Functions for multi-value trait analysis
  • pcv.joyplot
  • pcv.emd
  • pcv.net
  • conjugate
  • Resources

pcvr Goals

Currently pcvr aims to:

  • Make common tasks easier and consistent
  • Make select Bayesian statistics easier

There is room for goals to evolve based on feedback and scientific needs.

Load package

Pre-work was to install R, Rstudio, and pcvr with dependencies.

What are multi-value traits?

Sometimes a single value cannot describe a phenotype adequately.

What are multi-value traits?

Here our segmentation easily shows area, height, and other numeric phenotypes. To describe the color of this plant then we need a more complex phenotype.

What are multi-value traits?

There are many ways to describe color, many wavelengths to measure color in, and many indices that can be calculated from those wavelengths.

Since each pixel has a color we describe the entire image using a histogram of those values

Wikipedia HSV Color Space
Wikipedia HSV Color Space

Multi value trait format

PlantCV returns multi-value traits as histograms in long format

structure(list(sample = c(
  "default", "default", "default", "default",
  "default", "default", "default", "default", "default", "default",
  "default", "default", "default", "default", "default"
), trait = c(
  "hue_frequencies",
  "hue_frequencies", "hue_frequencies", "hue_frequencies", "hue_frequencies",
  "hue_frequencies", "hue_frequencies", "hue_frequencies", "hue_frequencies",
  "hue_frequencies", "hue_frequencies", "hue_frequencies", "hue_frequencies",
  "hue_frequencies", "hue_frequencies"
), value = c(
  0.805186656906828,
  1.04569695702186, 1.19906584405173, 1.76025654432012, 2.43647390986092,
  3.29220258635714, 4.97926034368573, 6.07201366377357, 8.33071909094078,
  8.61131444107498, 8.26100596047266, 7.65624455366168, 6.45543588134825,
  5.53347973090732, 5.05245913067726
), label = c(
  81L, 83L, 85L,
  87L, 89L, 91L, 93L, 95L, 97L, 99L, 101L, 103L, 105L, 107L, 109L
)), row.names = 3641:3655, class = "data.frame")
##       sample           trait     value label
## 3641 default hue_frequencies 0.8051867    81
## 3642 default hue_frequencies 1.0456970    83
## 3643 default hue_frequencies 1.1990658    85
## 3644 default hue_frequencies 1.7602565    87
## 3645 default hue_frequencies 2.4364739    89
## 3646 default hue_frequencies 3.2922026    91
## 3647 default hue_frequencies 4.9792603    93
## 3648 default hue_frequencies 6.0720137    95
## 3649 default hue_frequencies 8.3307191    97
## 3650 default hue_frequencies 8.6113144    99
## 3651 default hue_frequencies 8.2610060   101
## 3652 default hue_frequencies 7.6562446   103
## 3653 default hue_frequencies 6.4554359   105
## 3654 default hue_frequencies 5.5334797   107
## 3655 default hue_frequencies 5.0524591   109

Multi value trait format

In pcvr you can choose to read multi value traits in wide format with mode="wide" in read.pcv.

structure(list(hue_frequencies.45 = c(
  0.0154487872701993, 0,
  0, 0, 0
), hue_frequencies.47 = c(
  0, 0, 0, 0.0749063670411985,
  0
), hue_frequencies.49 = c(
  0.0308975745403986, 0.37593984962406,
  0.0774593338497289, 0, 0
), hue_frequencies.51 = c(
  0, 0, 0, 0,
  0.0657894736842105
)), row.names = 100:104, class = "data.frame")
##     hue_frequencies.45 hue_frequencies.47 hue_frequencies.49 hue_frequencies.51
## 100         0.01544879         0.00000000         0.03089757         0.00000000
## 101         0.00000000         0.00000000         0.37593985         0.00000000
## 102         0.00000000         0.00000000         0.07745933         0.00000000
## 103         0.00000000         0.07490637         0.00000000         0.00000000
## 104         0.00000000         0.00000000         0.00000000         0.06578947

. . .

Either option will work for most pcvr functions.

Functions for multi-value trait analysis

  • pcv.joyplot
  • pcv.emd
  • pcv.net
  • conjugate

Simulated data 

set.seed(123)
simFreqs <- function(vec, group) {
  s1 <- hist(vec, breaks = seq(1, 181, 1), plot = FALSE)$counts
  s1d <- as.data.frame(cbind(data.frame(group), matrix(s1, nrow = 1)))
  colnames(s1d) <- c("group", paste0("sim_", 1:180))
  s1d
}
sim_df <- rbind(
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(rnorm(200, 70, 10), group = "normal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(rlnorm(200, log(30), 0.35), group = "lognormal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(c(rlnorm(125, log(15), 0.25), rnorm(75, 75, 5)), group = "bimodal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(c(rlnorm(80, log(20), 0.3), rnorm(70, 70, 10), rnorm(50, 120, 5)), group = "trimodal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(runif(200, 1, 180), group = "uniform")
  }))
)
sim_df_long <- as.data.frame(data.table::melt(data.table::as.data.table(sim_df), id.vars = "group"))
sim_df_long$bin <- as.numeric(sub("sim_", "", sim_df_long$variable))

sim_plot <- ggplot(sim_df_long, aes(x = bin, y = value, fill = group), alpha = 0.25) +
  geom_col(position = "identity", show.legend = FALSE) +
  pcv_theme() +
  labs(x = "Color Histogram Bin") +
  theme(axis.title.y = element_blank()) +
  facet_wrap(~group)

Here we simulate wide data, then lengthen it for plotting.

sim_plot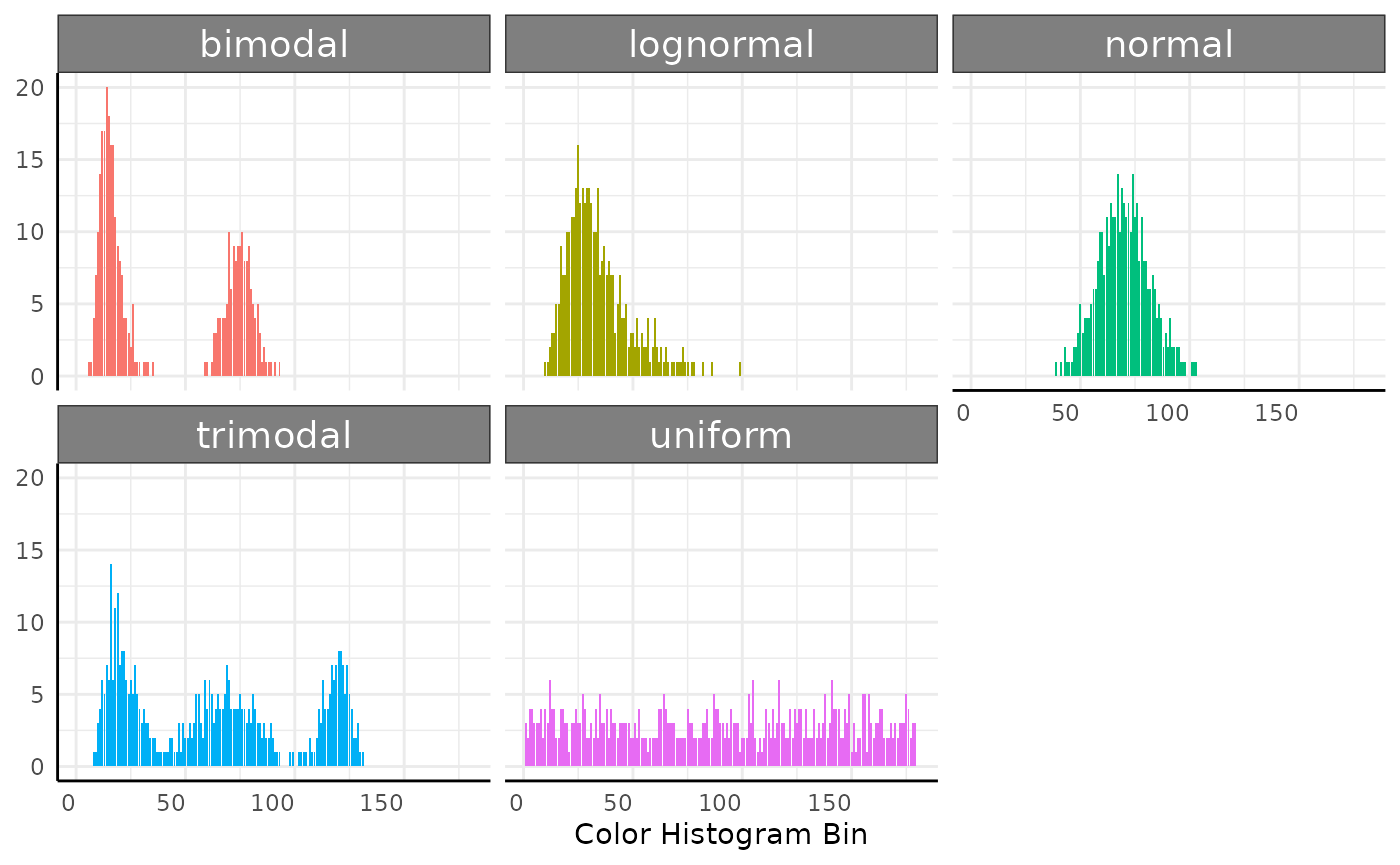

pcv.joyplot

We can make joyplots and using pcv.joyplot

(p <- pcv.joyplot(sim_df, index = "sim", group = c("group")))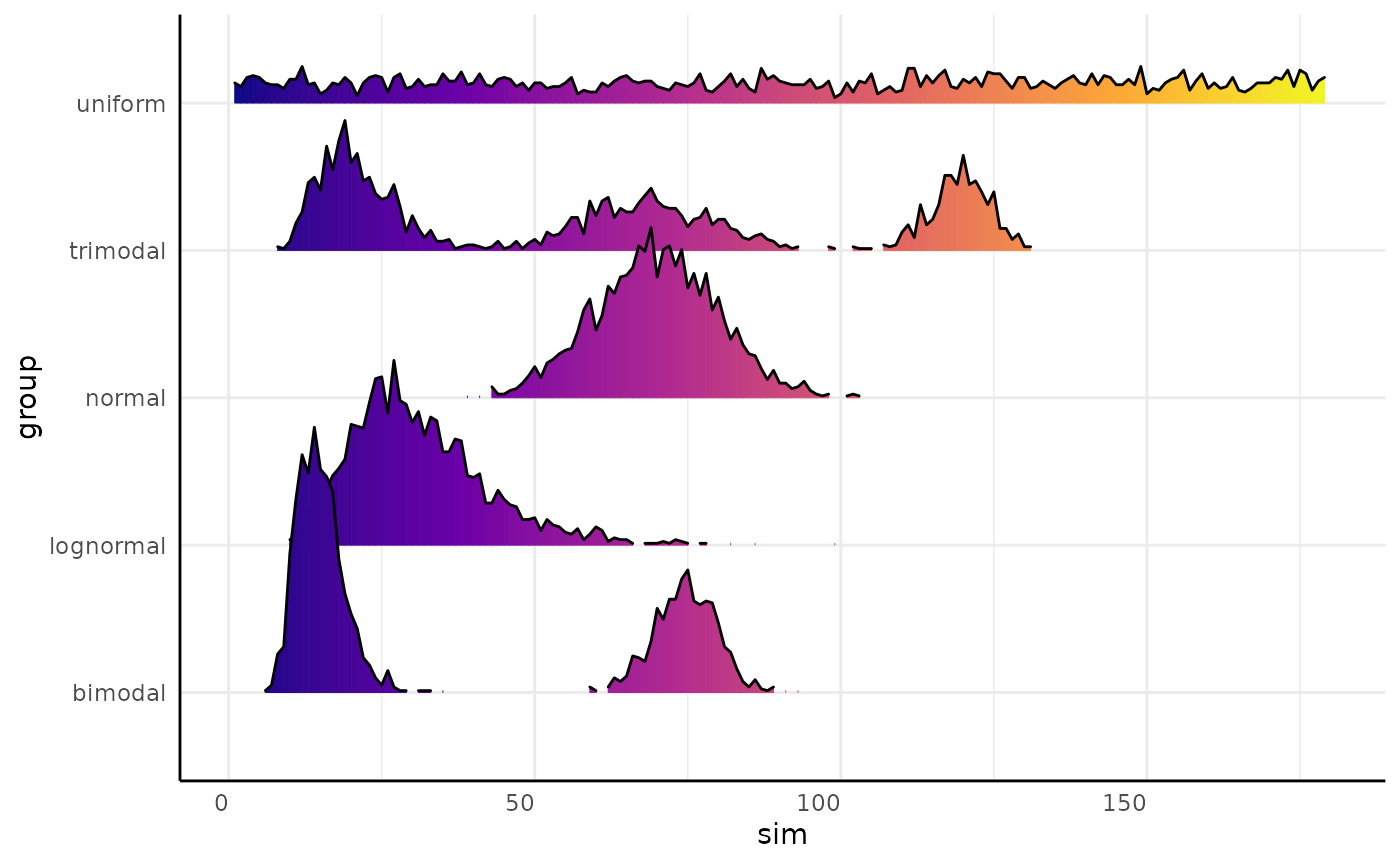

pcv.joyplot

The plot output is a ggplot object so we can change it to match our needs. Here we show these distributions as if they are hues.

p + scale_fill_gradientn(colors = scales::hue_pal(l = 55)(360))
## Scale for fill is already present.
## Adding another scale for fill, which will replace the existing scale.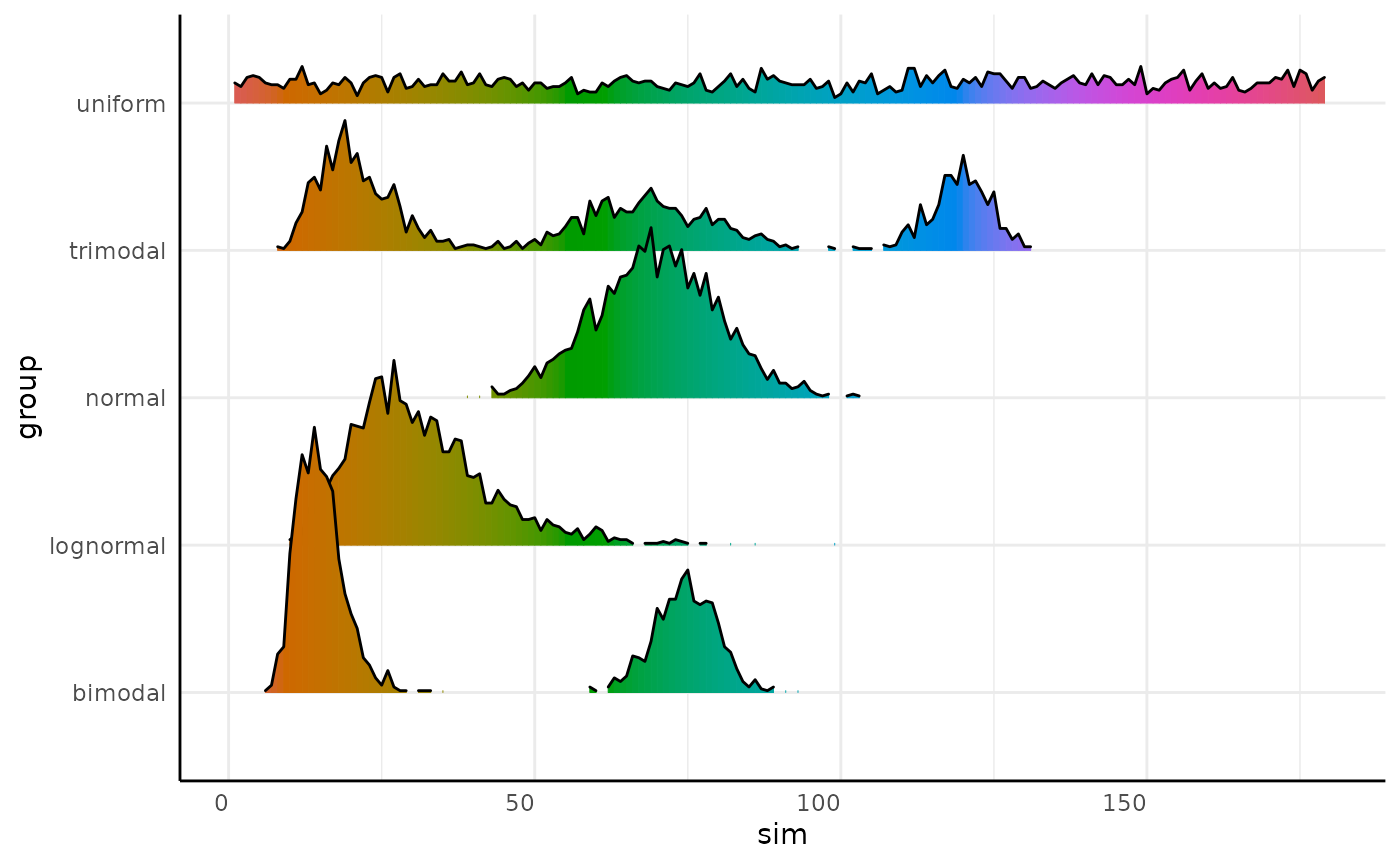

pcv.emd

Sometimes the multi-value trait histograms will not follow a unimodal distribution, or other aspects of what kind of test to use will be unclear.

For those situations one option is to use earth mover’s distance.

Earth Mover’s Distance

EMD measures the amount of work needed to change one histogram into another.

EMD then can be used to quantify the difference in color histograms.

Here the EMD would be 0.01 since only 1 count has to move 1 space out of 100 total observations:

#* visual of emd
set.seed(123)
df <- data.frame(x = round(runif(101, 1, 10)), y = c(rep("original", 99), "old", "new"))
df[100:101, "x"] <- c(5, 6)
p1 <- ggplot(df[df$y != "new", ], aes(x = x)) +
  geom_histogram(binwidth = 1, color = "white") +
  scale_x_continuous(breaks = c(1:10)) +
  scale_y_continuous(limits = c(0, 15)) +
  labs(title = "Sample 1", y = "Counts", x = "Bin") +
  pcv_theme()

p2 <- ggplot(df[df$y == "original", ], aes(x = x)) +
  geom_histogram(binwidth = 1, color = "white") +
  scale_x_continuous(breaks = c(1:10)) +
  scale_y_continuous(limits = c(0, 15)) +
  geom_rect(
    data = data.frame(x = 1), aes(xmin = 4.5, xmax = 5.5, ymin = 14, ymax = 15),
    fill = "blue", color = "white", alpha = 0.25
  ) +
  geom_rect(
    data = data.frame(x = 1), aes(xmin = 5.5, xmax = 6.5, ymin = 6, ymax = 7),
    fill = "red", color = "white", alpha = 1
  ) +
  labs(title = "Sample 2") +
  labs(x = "Bin") +
  pcv_theme() +
  theme(
    axis.line.y.left = element_blank(),
    axis.title.y = element_blank(),
    axis.text.y = element_blank()
  )

p1 + p2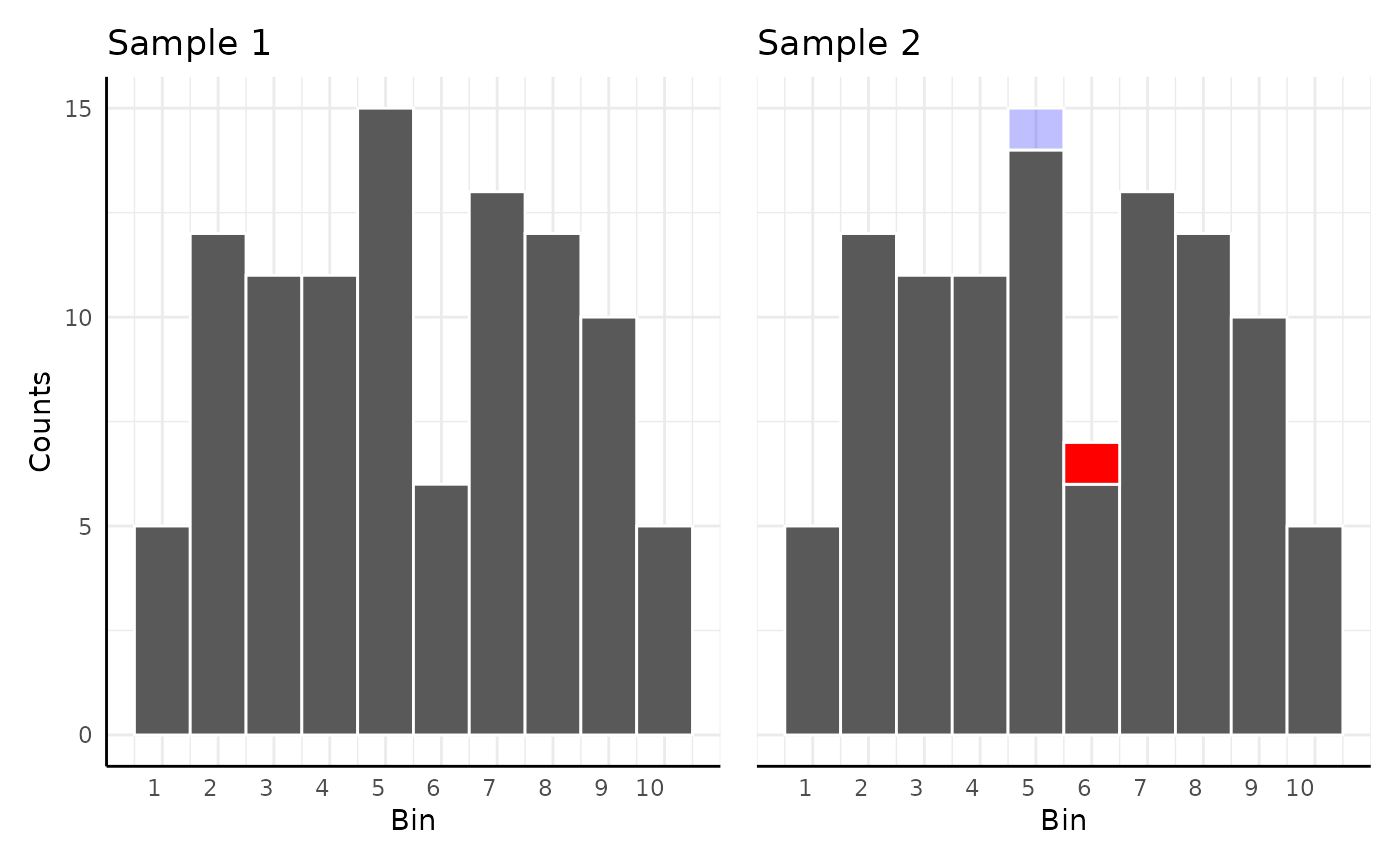

pcv.emd

Here we use the wide data (although long can also be used).

The “reorder” argument specifies groups to arrange together in the resulting plot if plot=TRUE.

If mat=TRUE then a distance matrix is returned, otherwise a long dataframe is returned.

For details see ?pcv.emd

sim_emd <- pcv.emd(
  df = sim_df, cols = "sim_", reorder = c("group"),
  mat = FALSE, plot = TRUE, parallel = 1, raiseError = FALSE
)

pcv.emd

Looking at the plot we can see that there are obvious differences between groups in our data.

sim_emd$plot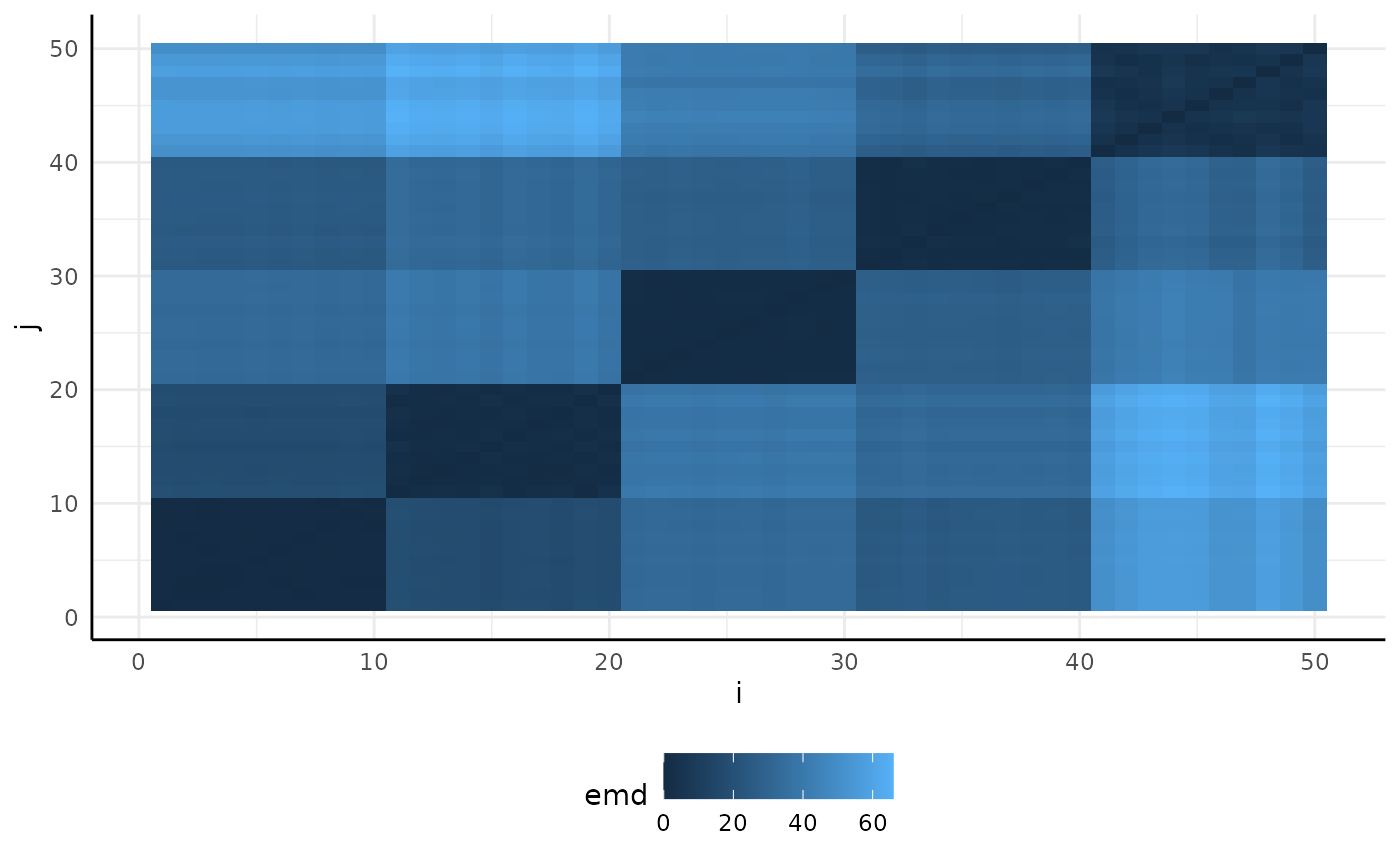

pcv.net

With non-matrix pcv.emd output we can make a network to better understand the color similarities in our data. Here we include a numeric filter which removes edges with an EMD below that value.

Note that the default behavior changes EMD from a distance to a dissimilarity.

set.seed(123)
n <- pcv.net(sim_emd$data, filter = 0.5)
lapply(n, class)
## $nodes
## [1] "data.frame"
## 
## $edges
## [1] "data.frame"
## 
## $graph
## [1] "igraph"

net.plot

Now we can visualize our network using net.plot.

net1 <- net.plot(n, fill = "group") +
  labs(color = "", title = "Network 1") +
  theme(plot.title = element_text(hjust = 0.5)) +
  scale_color_discrete(limits = c(
    "bimodal", "lognormal", "normal",
    "trimodal", "uniform"
  ))

net.plot

Our results show very clear clustering and highlight that the uniform distribution is most dissimilar to the others since it is excluded entirely. We can make another network to include it.

net1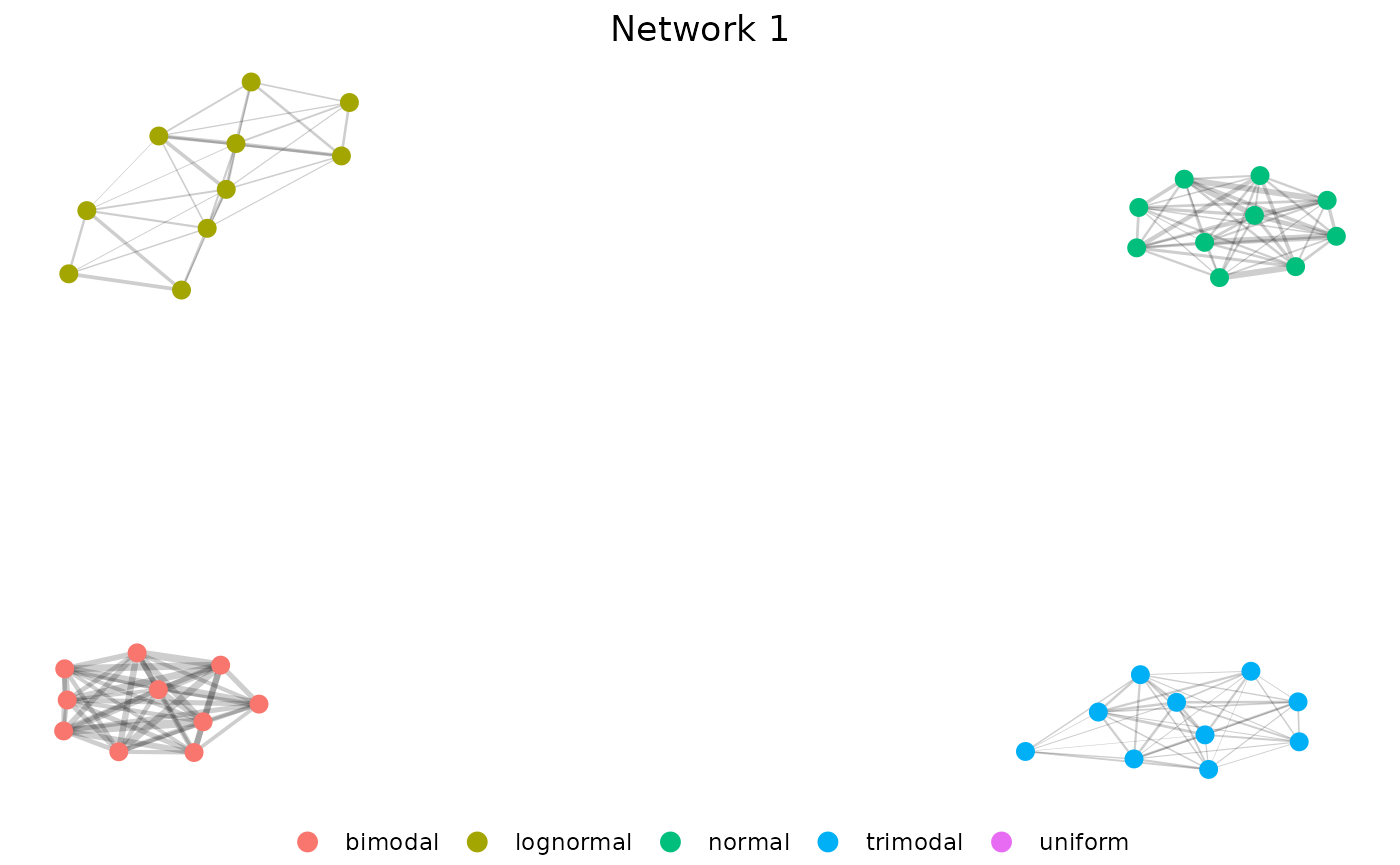

pcv.net

Here we specify our filter as a character, which is interpreted as a quantile here keeping only edges that are above median strength.

set.seed(123)
n <- pcv.net(sim_emd$data, filter = "0.5")
net2 <- net.plot(n, fill = "group") +
  labs(color = "", title = "Network 2") +
  theme(
    plot.title = element_text(hjust = 0.5),
    legend.position = "bottom"
  )

pcv.net

Now we can see the full layout of our five distributions.

net2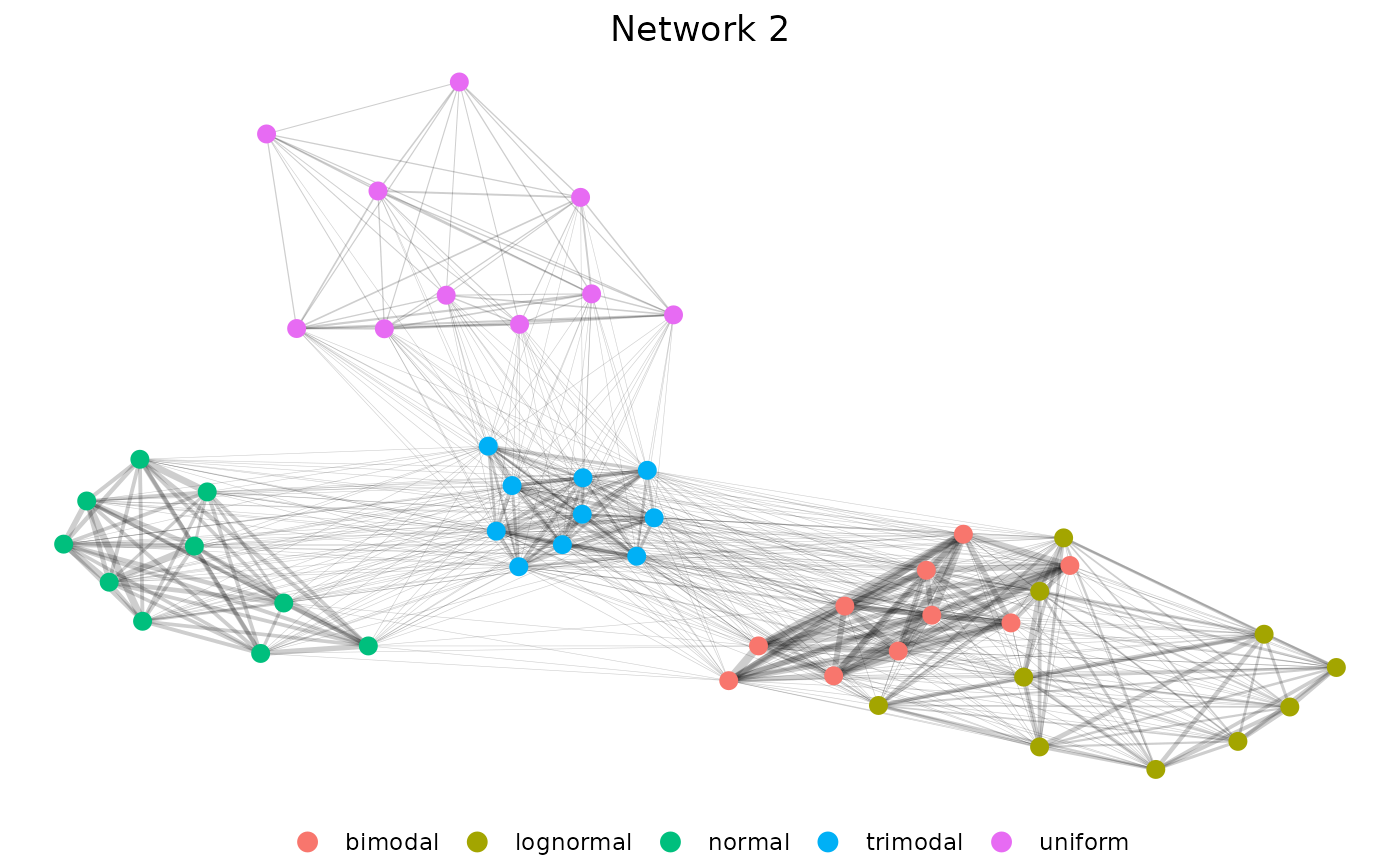

conjugate

Sometimes your distributions follow a parameterized distribution in which case more robust comparisons are possible.

The conjugate function can compare “t” (gaussian means), “gaussian”, “beta”, “lognormal”, “dirichlet”, and “dirichlet2” distributions of multi-value traits.

conjugate

Multi-value traits can be provided to conjugate as matrices. Here we subset our data to two samples.

s1 <- sim_df[sim_df$group == "normal", grepl("sim", colnames(sim_df))]
s2 <- sim_df[sim_df$group == "lognormal", grepl("sim", colnames(sim_df))]

conjugate

Now we can run conjugate on our samples. Here we use assume a lognormal distribution.

res <- conjugate(s1, s2,
  method = "lognormal",
  priors = list(mu = 10, sd = 5),
  plot = TRUE, rope_range = NULL, rope_ci = 0.89,
  cred.int.level = 0.89, hypothesis = "equal", support = NULL
)

conjugate

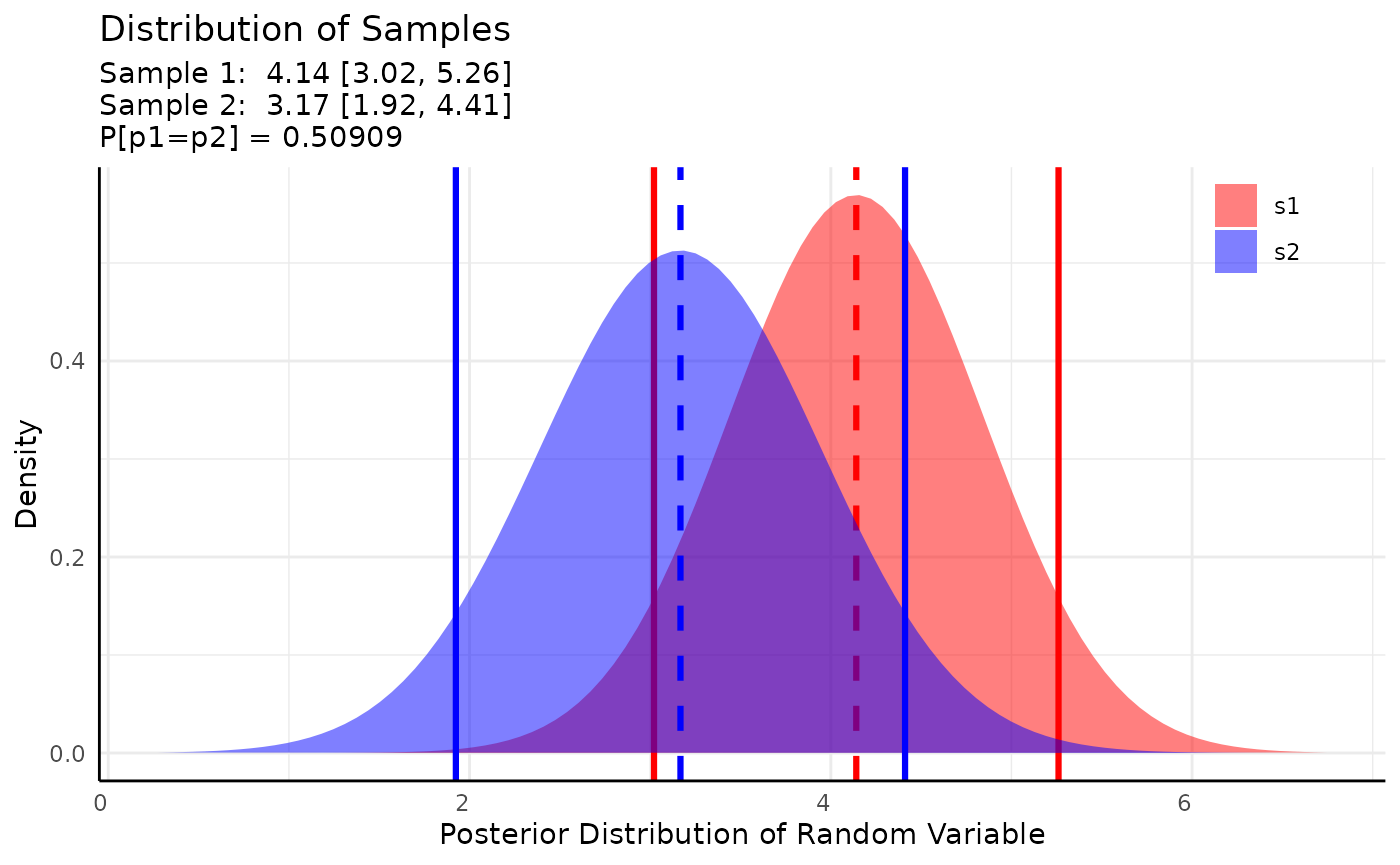
We can also perform region of practical equivalence tests by specifying a rope_range.

res <- conjugate(s1, s2,
  method = "lognormal",
  priors = list(mu = 10, sd = 5),
  plot = TRUE, rope_range = c(-10, 10), rope_ci = 0.89,
  cred.int.level = 0.89, hypothesis = "equal", support = NULL
)

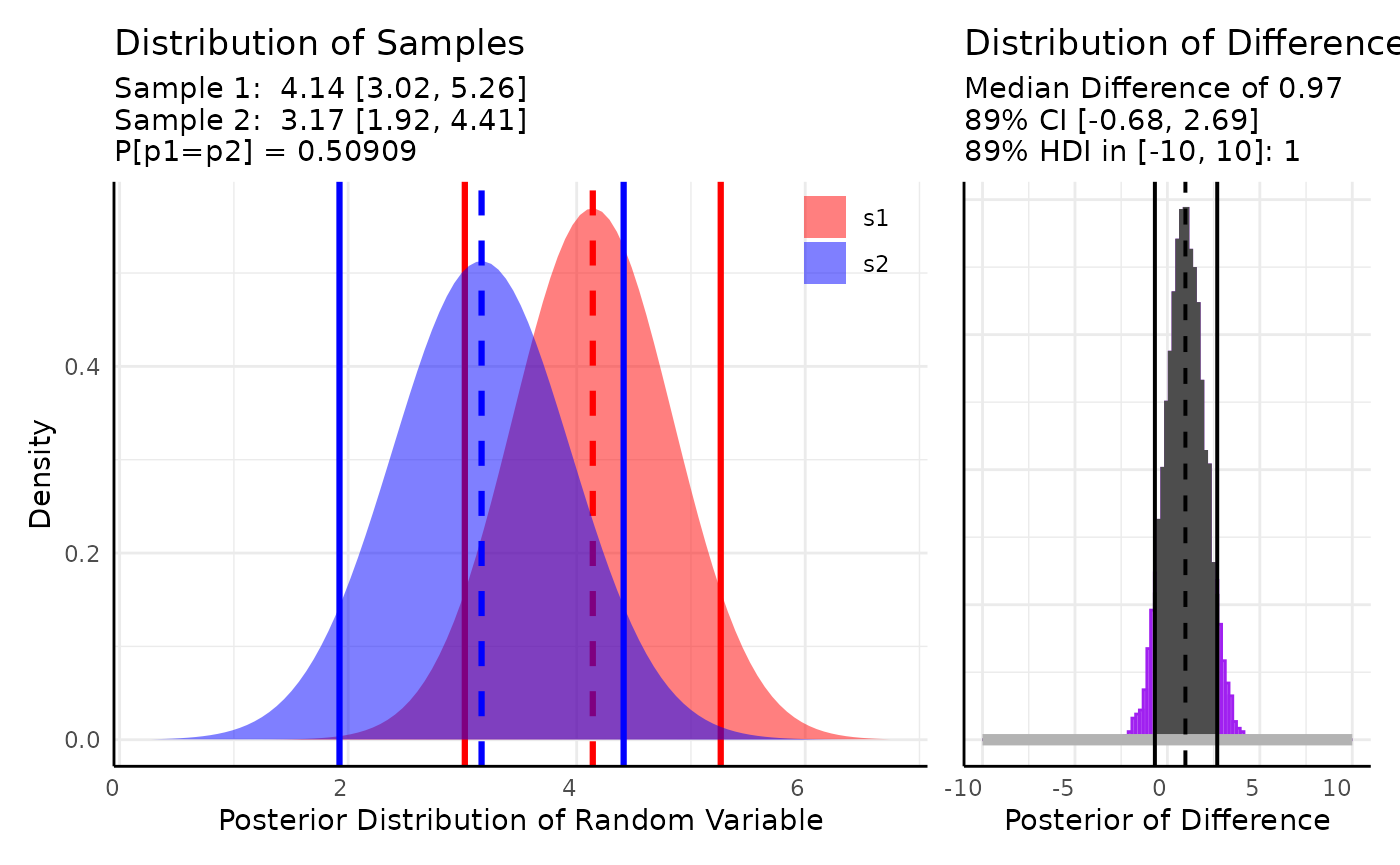
conjugate

The results are also returned as a summary dataframe

res$summary[, -c(1:6)]
##     hyp post.prob  HDE_rope HDI_rope_low HDI_rope_high rope_prob
## 1 equal 0.1676276 0.9725031    0.2023803      1.807437         1

Resources

If you run into a novel situation please reach out and we will try to come up with a solution and add it to pcvr if possible.

Good ways to reach out are the help-datascience slack channel and pcvr github repository.