Skip to contents

Intermediate Growth Modeling with `pcvr`

pcvr v1.0.0

Josh Sumner

Source: vignettes/articles/pcvrTutorial_igm.Rmd
pcvrTutorial_igm.Rmd

Outline

  • pcvr Goals
  • Load Package
  • Why Longitudinal Modeling?
  • Supported Model Builders
  • Supported Curves
  • growthSS
  • fitGrowth
  • growthPlot
  • testGrowth
  • Resources

pcvr Goals

Currently pcvr aims to:

  • Make common tasks easier and consistent
  • Make select Bayesian statistics easier

There is room for goals to evolve based on feedback and scientific needs.

Load package

Pre-work was to install R, Rstudio, and pcvr with dependencies.

library(pcvr) # or devtools::load_all() if you are editing
library(ggplot2)
library(patchwork)

Why Longitudinal Modeling?

plantCV allows for user friendly high throughput image based phenotyping

Resulting data follows individuals over time, which changes our statistical needs.

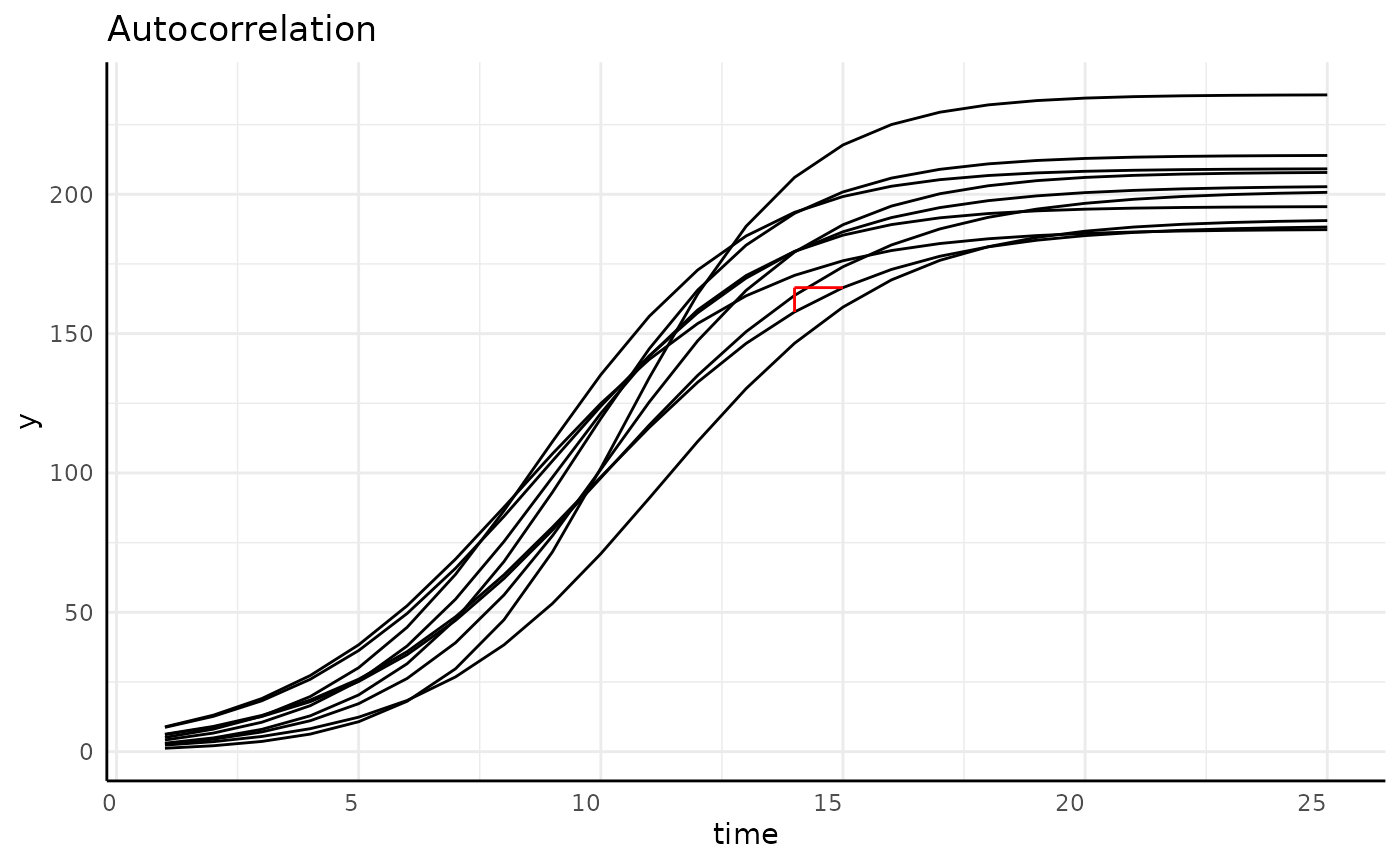
Longitudinal Data is:

  • Autocorrelated
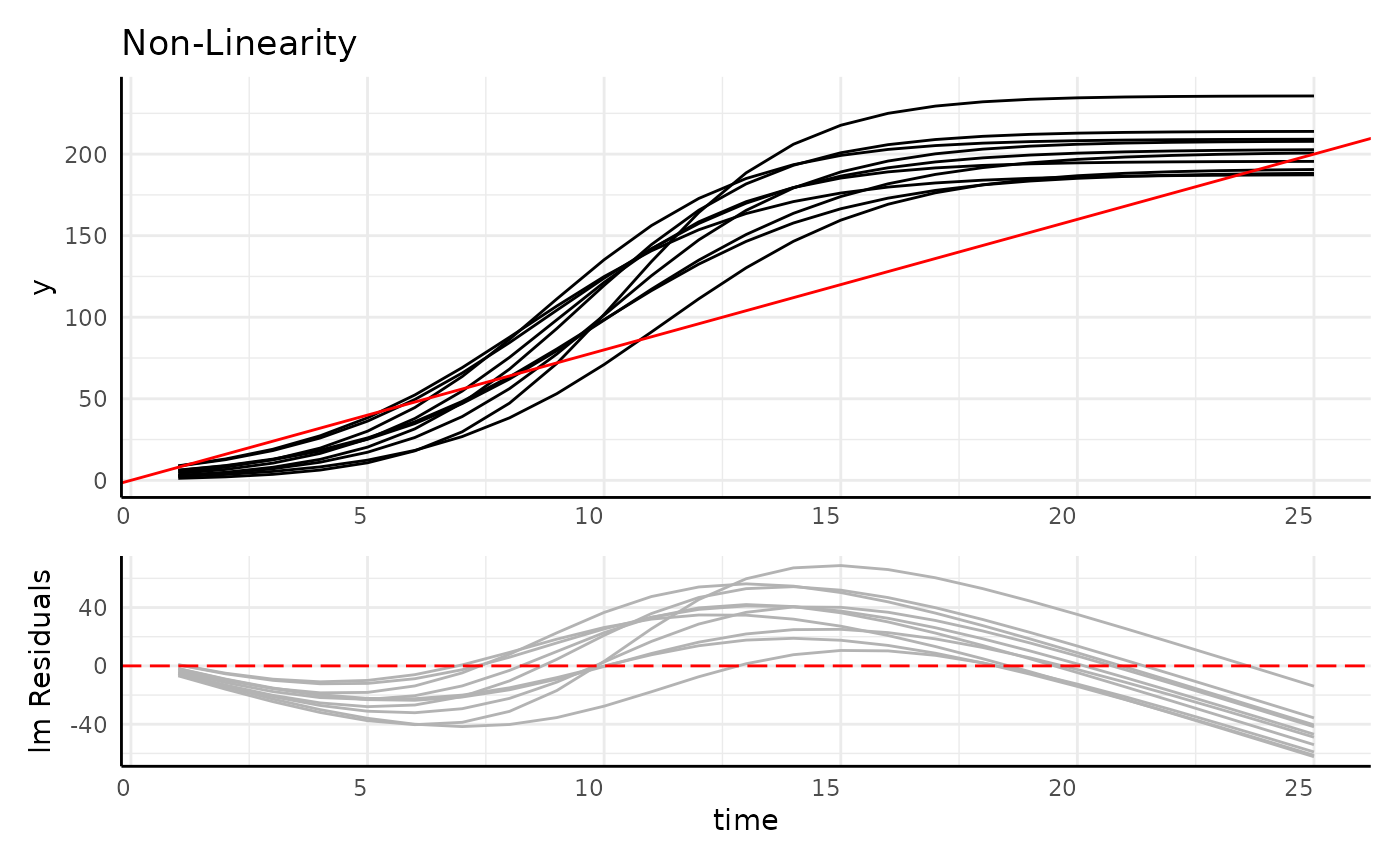
  • Often non-linear
  • Heteroskedastic

Highlighting autocorrelation as a feature of longitudinal data

Highlighting non-linearyity as a common feature of longitudinal data

r1 <- range(simdf[simdf$time == 1, "y"])
r2 <- range(simdf[simdf$time == 5, "y"])
r3 <- range(simdf[simdf$time == 10, "y"])
r4 <- range(simdf[simdf$time == 20, "y"])

main <- ggplot(simdf, aes(time, y, group = interaction(group, id))) +
  geom_line() +
  annotate("segment", x = 1, xend = 1, y = r1[1], yend = r1[2], color = "blue", linewidth = 2) +
  annotate("segment", x = 5, xend = 5, y = r2[1], yend = r2[2], color = "blue", linewidth = 2) +
  annotate("segment", x = 10, xend = 10, y = r3[1], yend = r3[2], color = "blue", linewidth = 2) +
  annotate("segment", x = 20, xend = 20, y = r4[1], yend = r4[2], color = "blue", linewidth = 2) +
  labs(title = "Heteroskedasticity") +
  pcv_theme() +
  theme(axis.title.x = element_blank(), axis.text.x = element_blank())

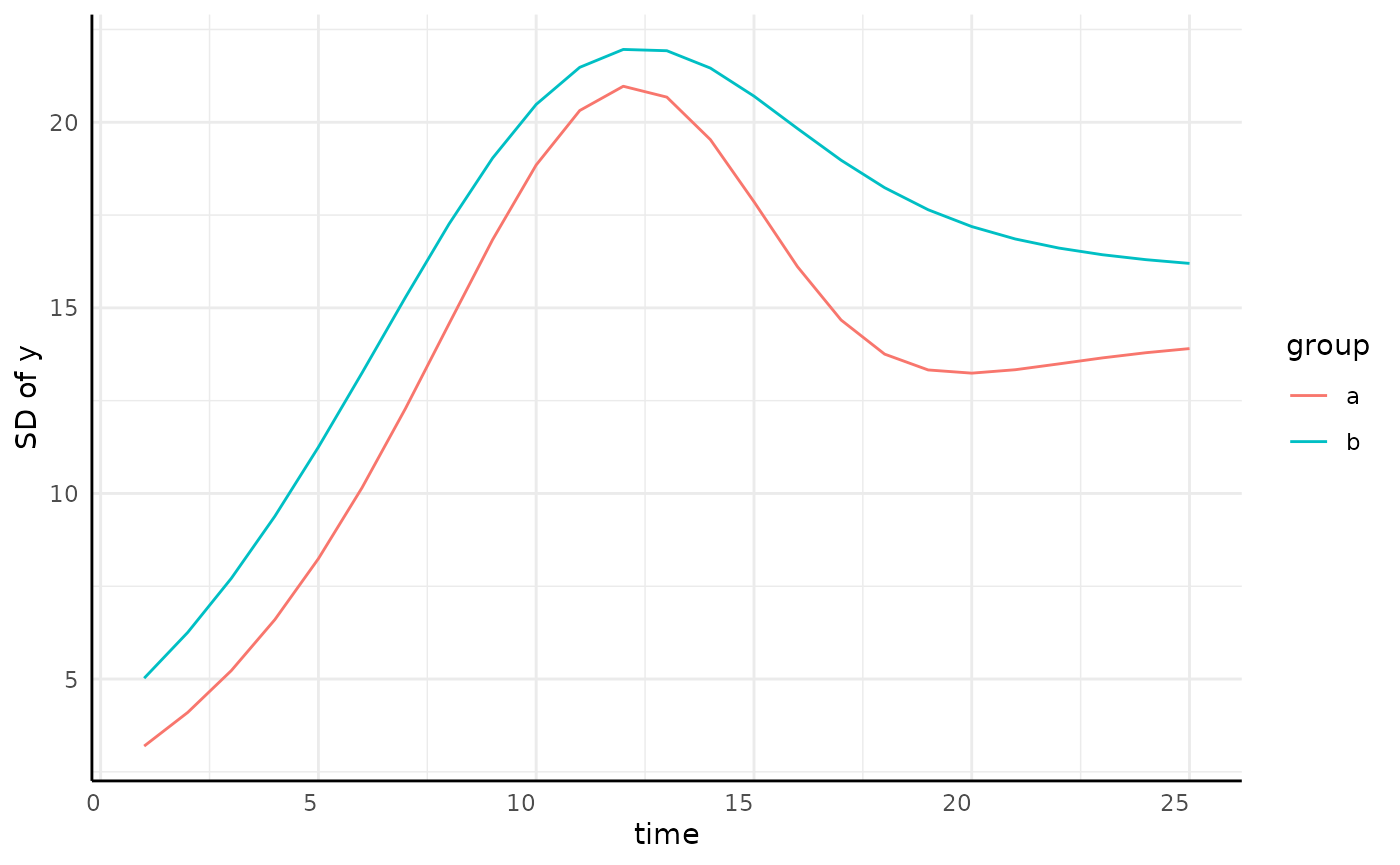
sigma_df <- aggregate(y ~ group + time, data = simdf, FUN = sd)

sigmaPlot <- ggplot(sigma_df, aes(x = time, y = y, group = group)) +
  geom_line(color = "blue") +
  pcv_theme() +
  labs(y = "SD of y") +
  theme(plot.title = element_blank())


design <- c(
  area(1, 1, 4, 4),
  area(5, 1, 6, 4)
)
hetPatch <- main / sigmaPlot + plot_layout(design = design)
hetPatch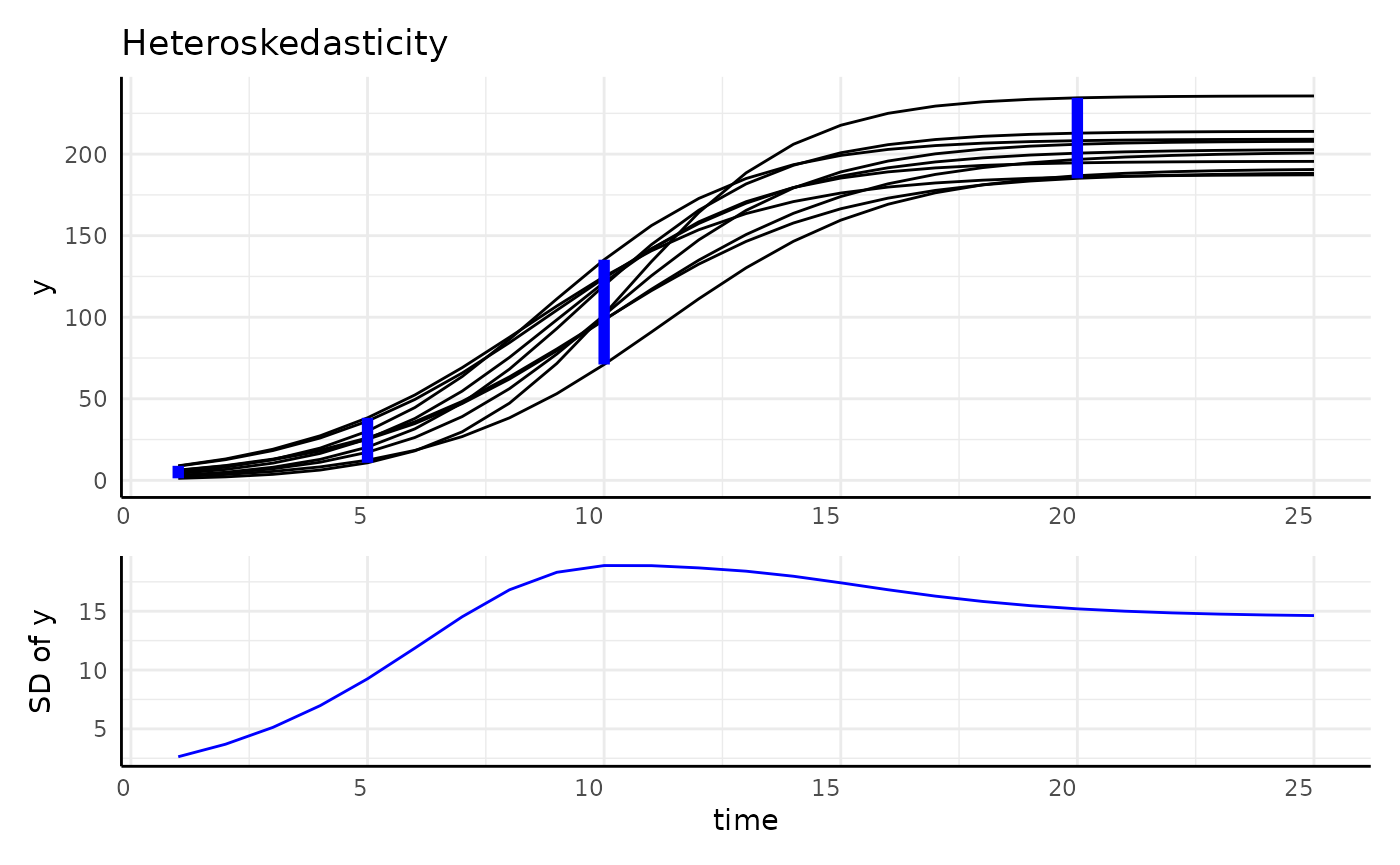

Highlighting heteroskedasticity as a nearly ubiquitous feature of longitudinal data

Supported Model Builders

Five model building options are supported through the type argument of growthSS:

nls, nlrq, nlme, mgcv, and brms

Other than mgcv all model builders can fit 9 types of growth models.

Supported Model Builders 2

“nls” “nlrq” “nlme” “mgcv” “brms”
stats::nls quantreg::nlrq nlme::nlme mgcv::gam brms::brms

type = “nls”

Non-linear least squares regression.

Longitudinal Trait nls
Non-linearity ✅
Autocorrelation ❌
Heteroskedasticity ❌

type = “nlrq”

Linear Regression Quantile Regression
Predicts mean E(Y|X) Predicts quantiles Q(Y|X)
Works with small N Requires higher N
Assumes Normality No distributional assumptions
E(Y|X) breaks with transformation Q(Y|X) robust to transformation
Sensitive to outliers Robust to outliers
Computationally cheap Computationally more expensive

type = “nlrq”

Non-linear quantile regression.

Longitudinal Trait nlrq
Non-linearity ✅
Autocorrelation ❌
Heteroskedasticity ✅

type = “nlme”

Non-linear Mixed Effect Models

Longitudinal Trait nlme
Non-linearity ✅
Autocorrelation* ✅
Heteroskedasticity ✅
Being a headache ✅

type = “mgcv”

General Additive Models Only

Longitudinal Trait gam
Non-linearity ✅
Autocorrelation ❌
Heteroskedasticity ❌
Unparameterized ✅

type = “brms”

Bayesian hierarchical Models

Longitudinal Trait brms
Non-linearity ✅
Autocorrelation ✅
Heteroskedasticity ✅

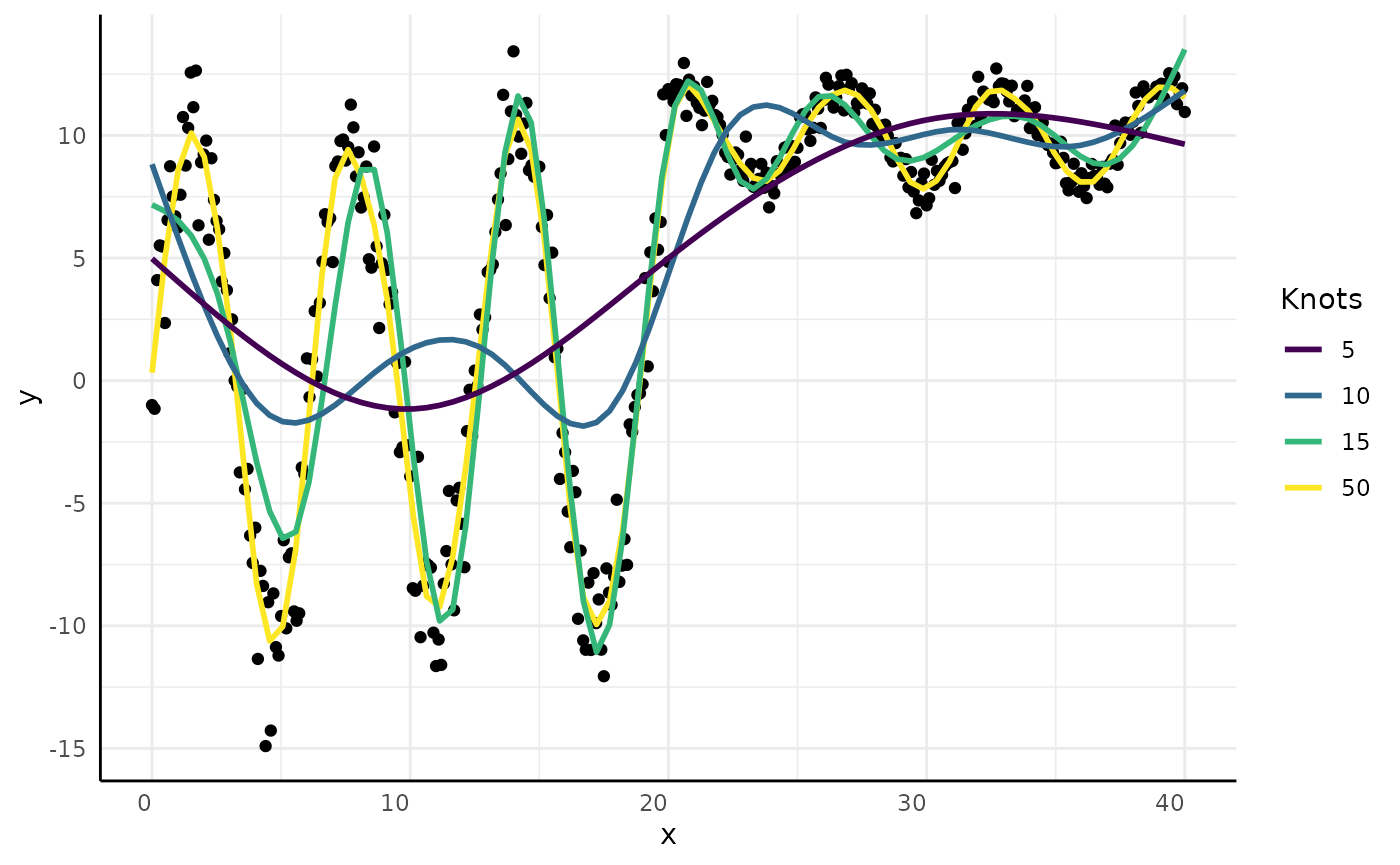
Supported Growth Models

There are 6 main growth models supported in pcvr, although there are several other options as well as changepoint models made of combinations between them.

Of the general 6 we are looking at, 3 are asymptotic, 3 are non-asympototic.

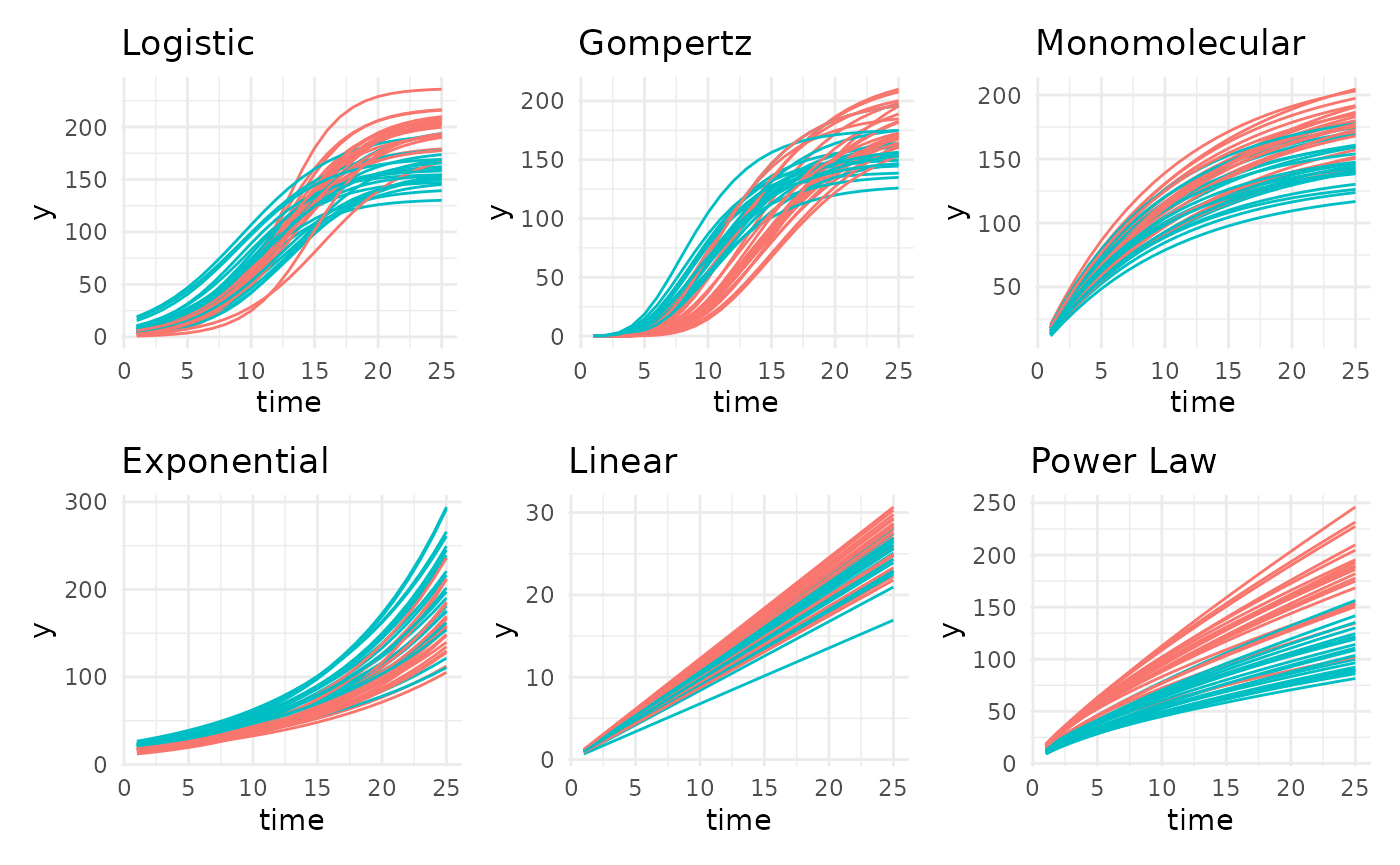
Showing 3 examples of asymptotic and 3 examples of non-asymptotic growth curves that are supported by pcvr.

Supported Growth Models

There are an additional 3 sigmoidal models based on the Extreme Value Distribution. Those are Weibull, Frechet, and Gumbel. The authors generally prefer Gompertz to these options but for your data it is possible that these could be a better fit.

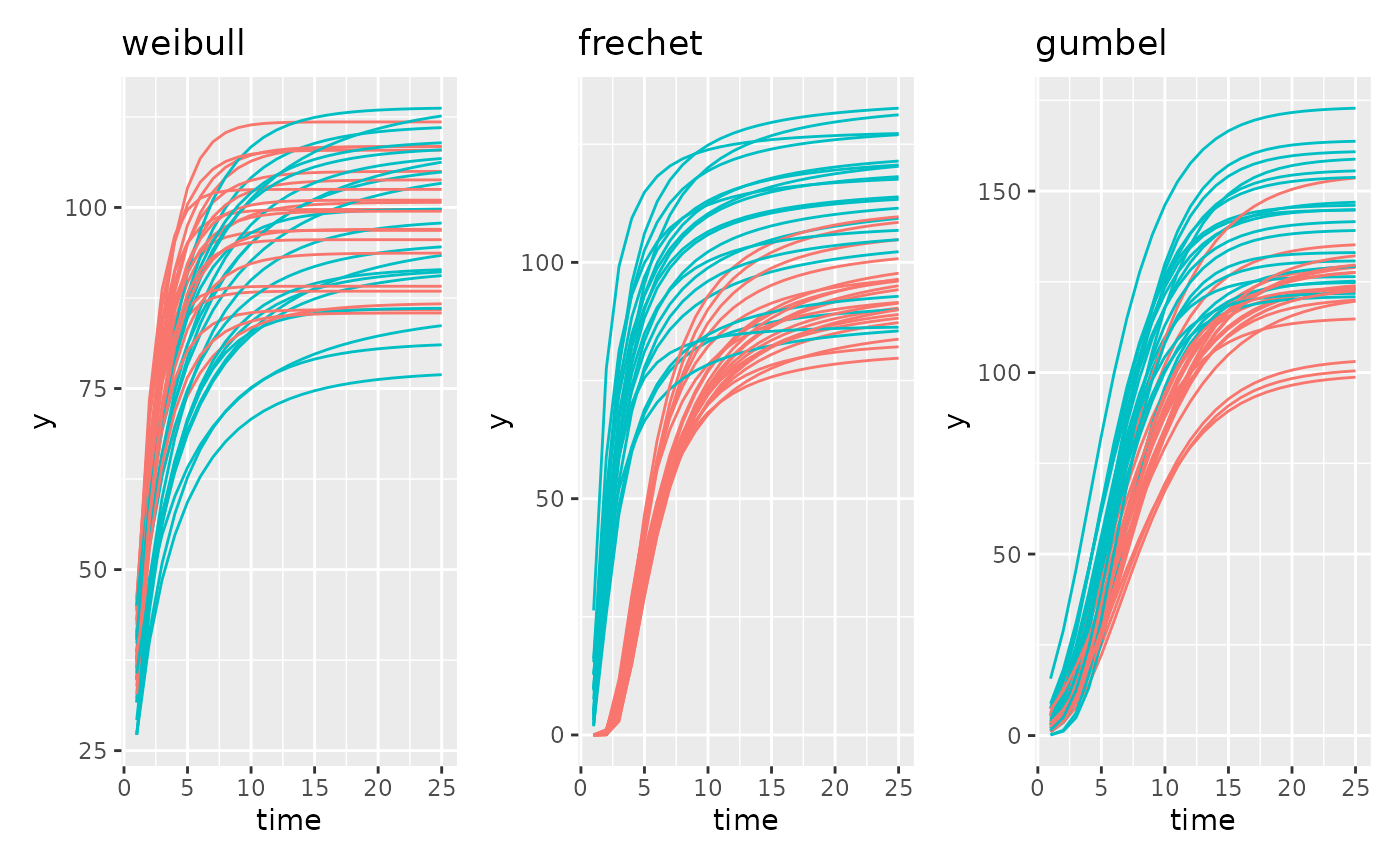
Showing variations of the Extreme Value Distribution sigmoid curves that are supported.

Supported Growth Models 2

There are also two double sigmoid curves intended for use with recovery experiments.

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).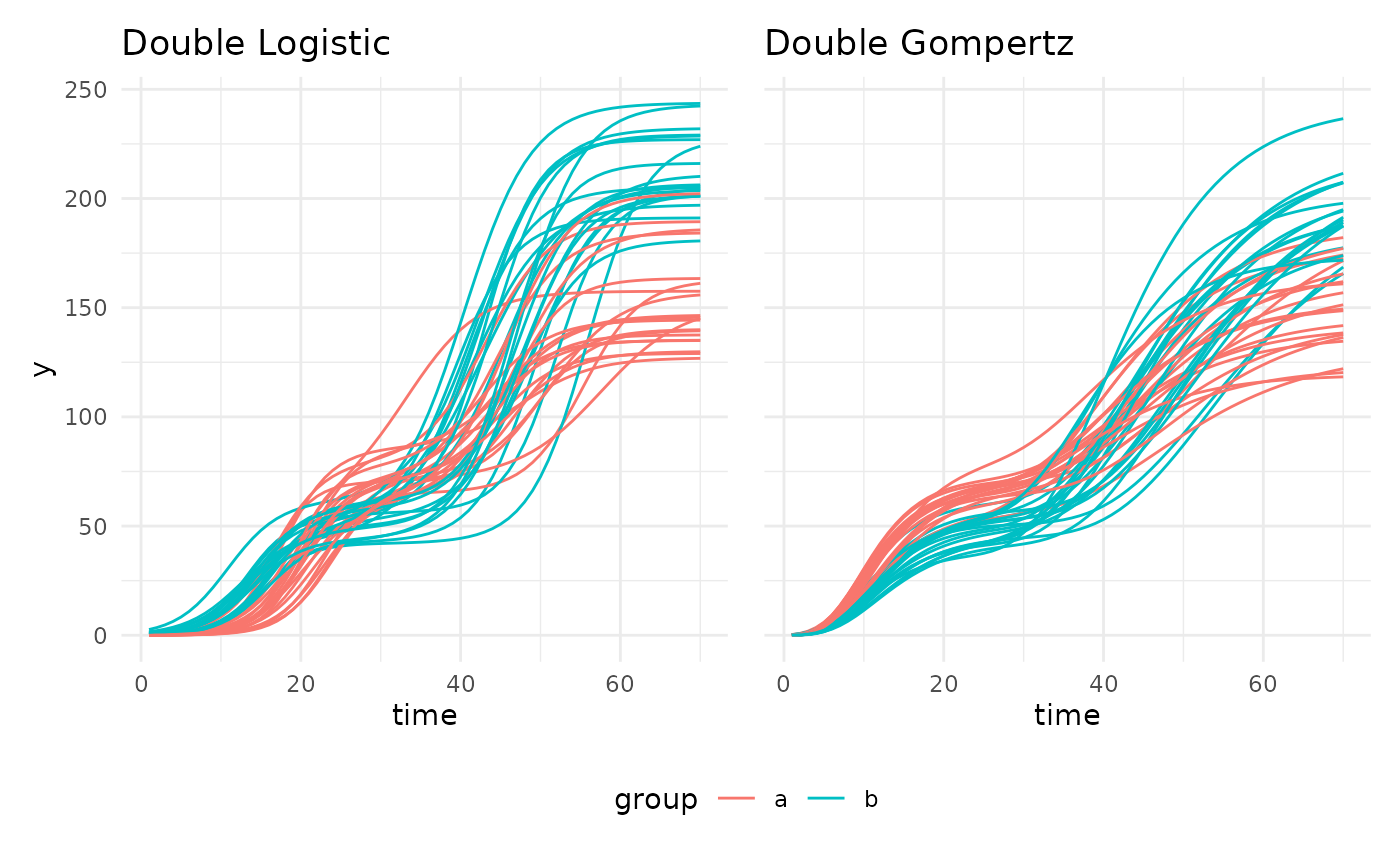

Two examples of multi-part models that can be parameterized without changepoints.

Supported Growth Models 3

Generalized Additive Models (GAMs) are also supported.

Example of the effect of changing the number of knots in a spline, with more knots being more prone to overfitting and fewer knots being less accurate for the observed data.

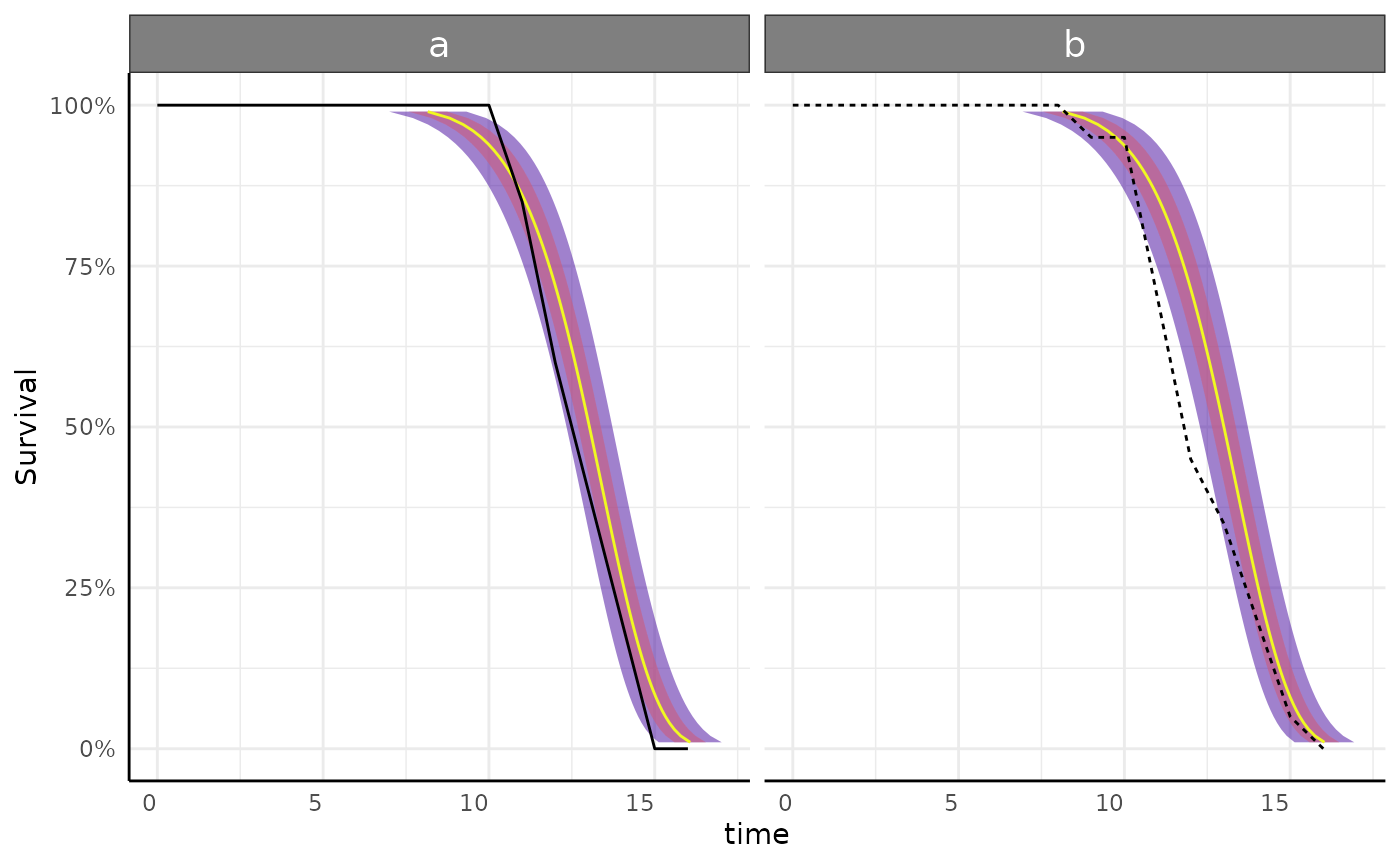
Survival Models

Survival models can also be specified using the “survival” keyword. These models can use the “survival” or “flexsurv” backends where distributions can be specified as model = "survival {distribution}".

For details please see the growthSS documentation.

GAMs 

m <- mgcv::gam(y ~ group + s(time, by = factor(group)), data = simdf)
start <- min(simdf$time)
end <- max(simdf$time)
support <- expand.grid(
  time = seq(start, end, length = 400),
  group = factor(unique(simdf$group))
)

out <- gam_diff(
  model = m, newdata = support, g1 = "a", g2 = "b",
  byVar = "group", smoothVar = "time", plot = TRUE
)

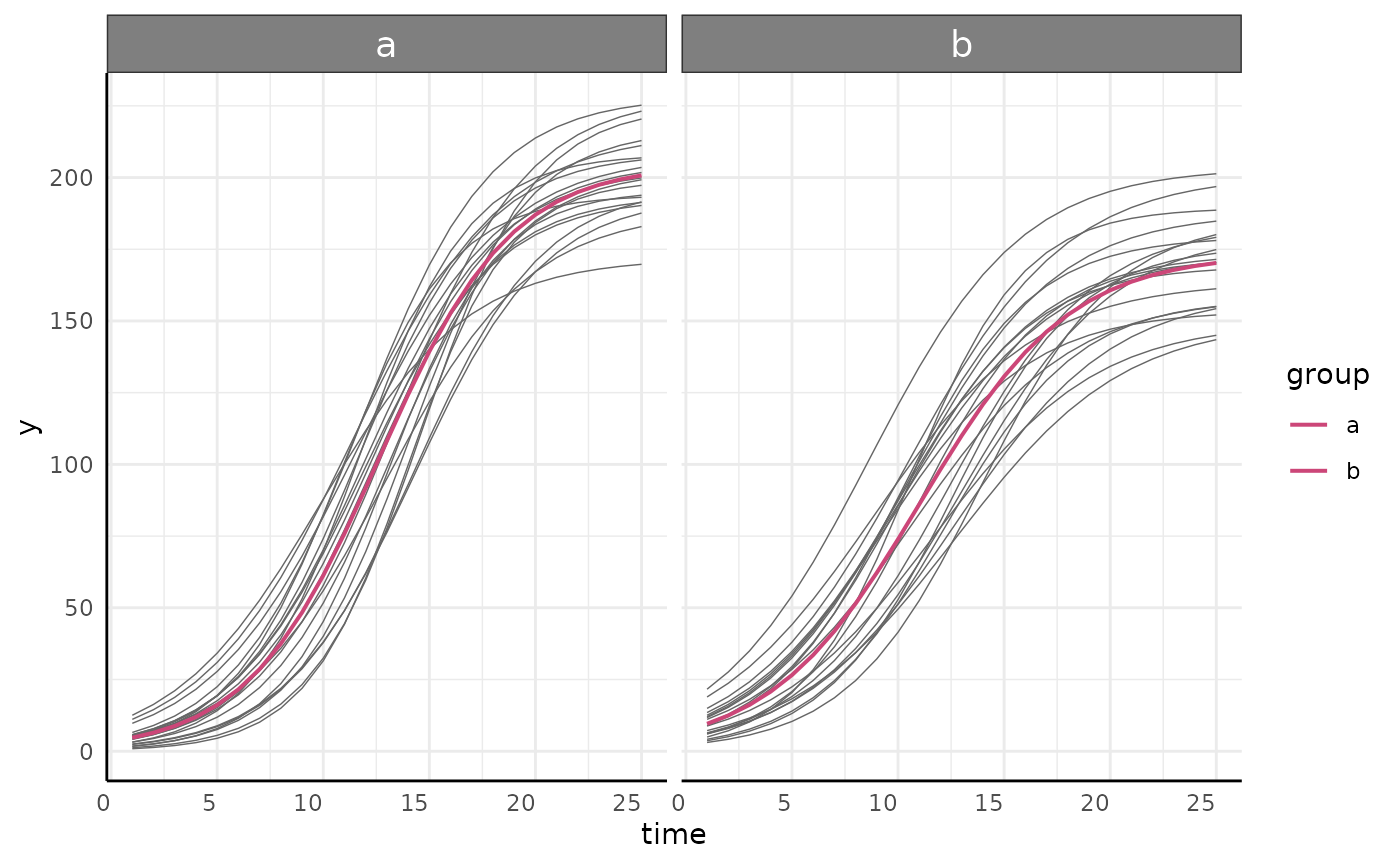
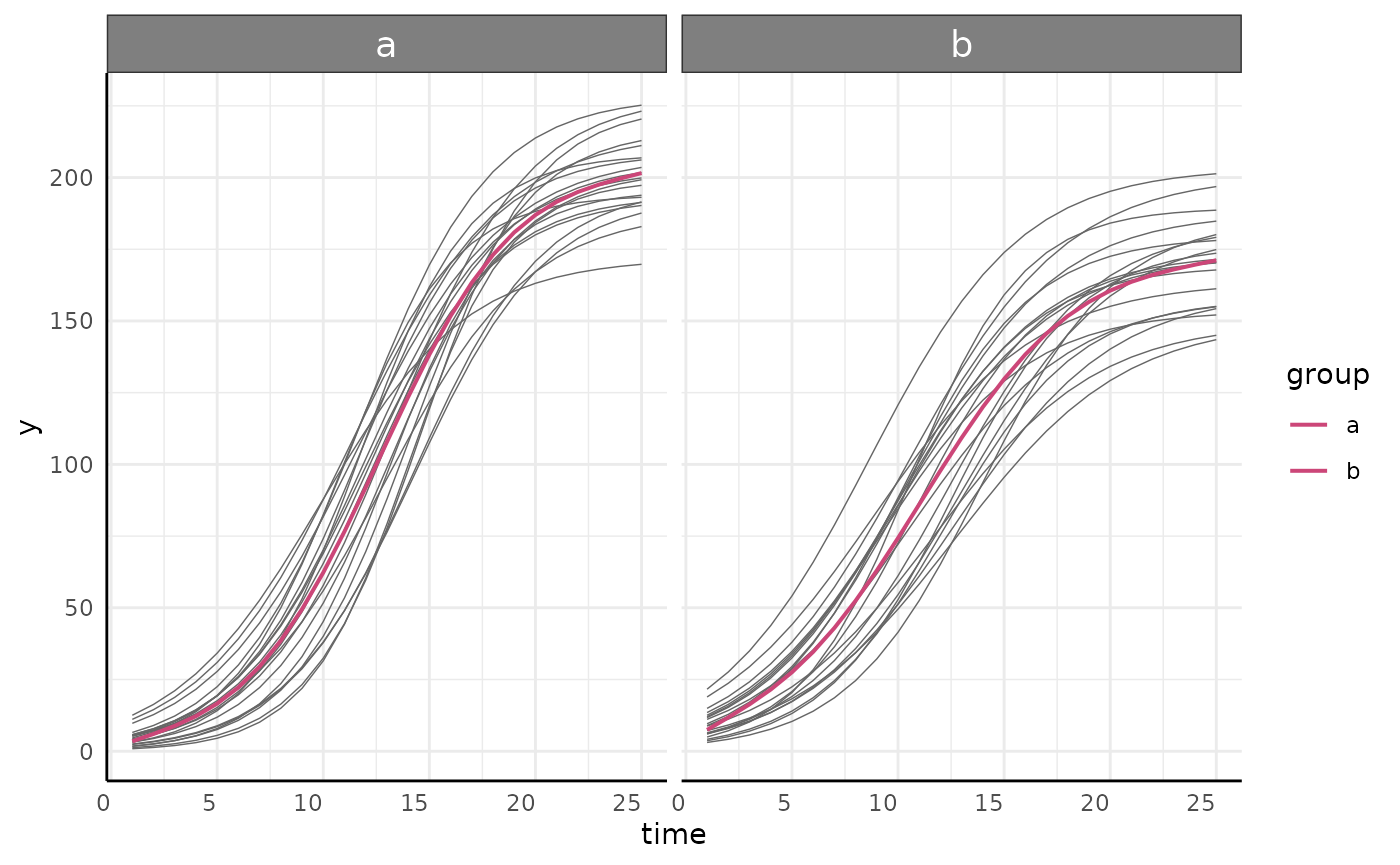
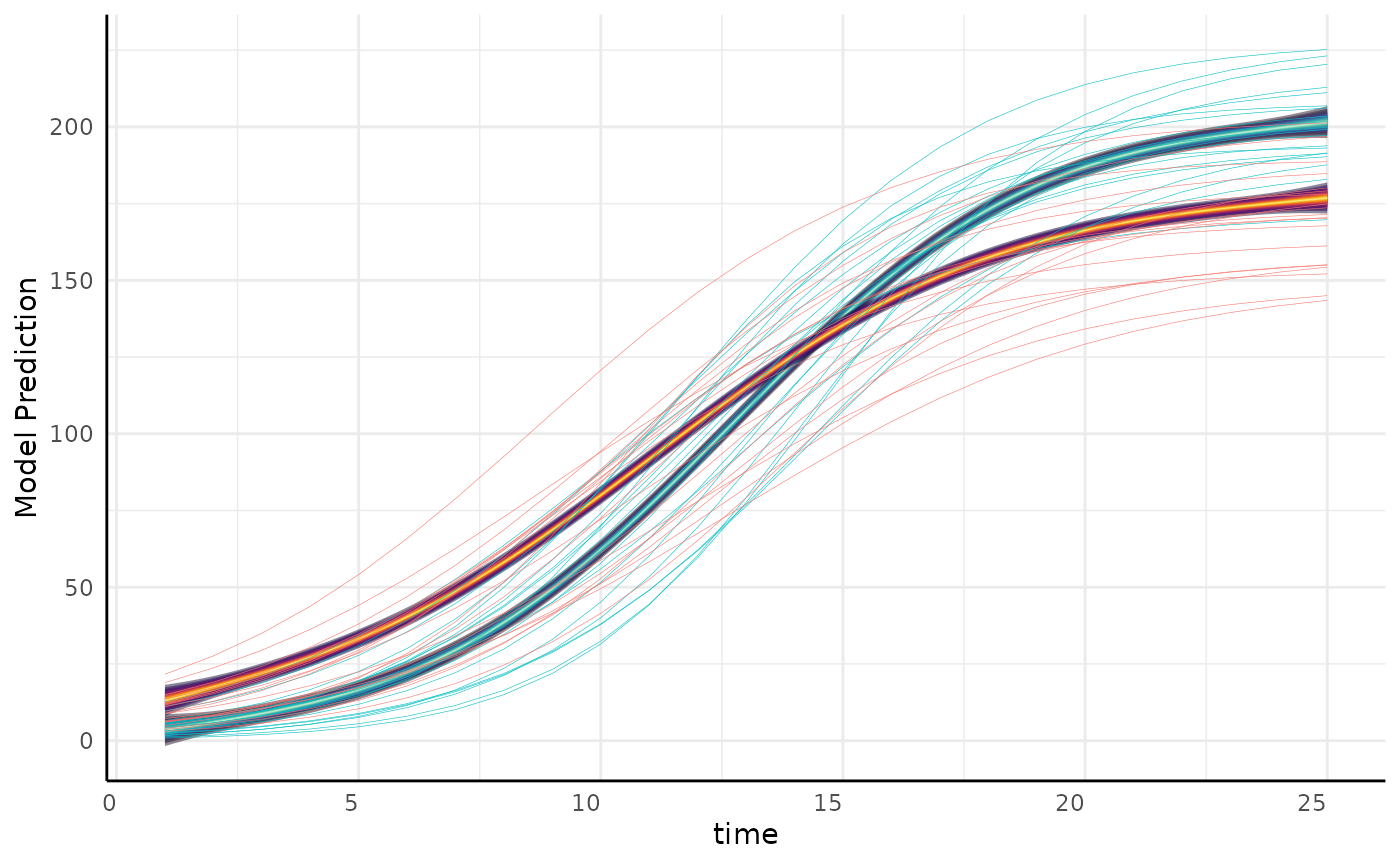
gam_diff predictions 

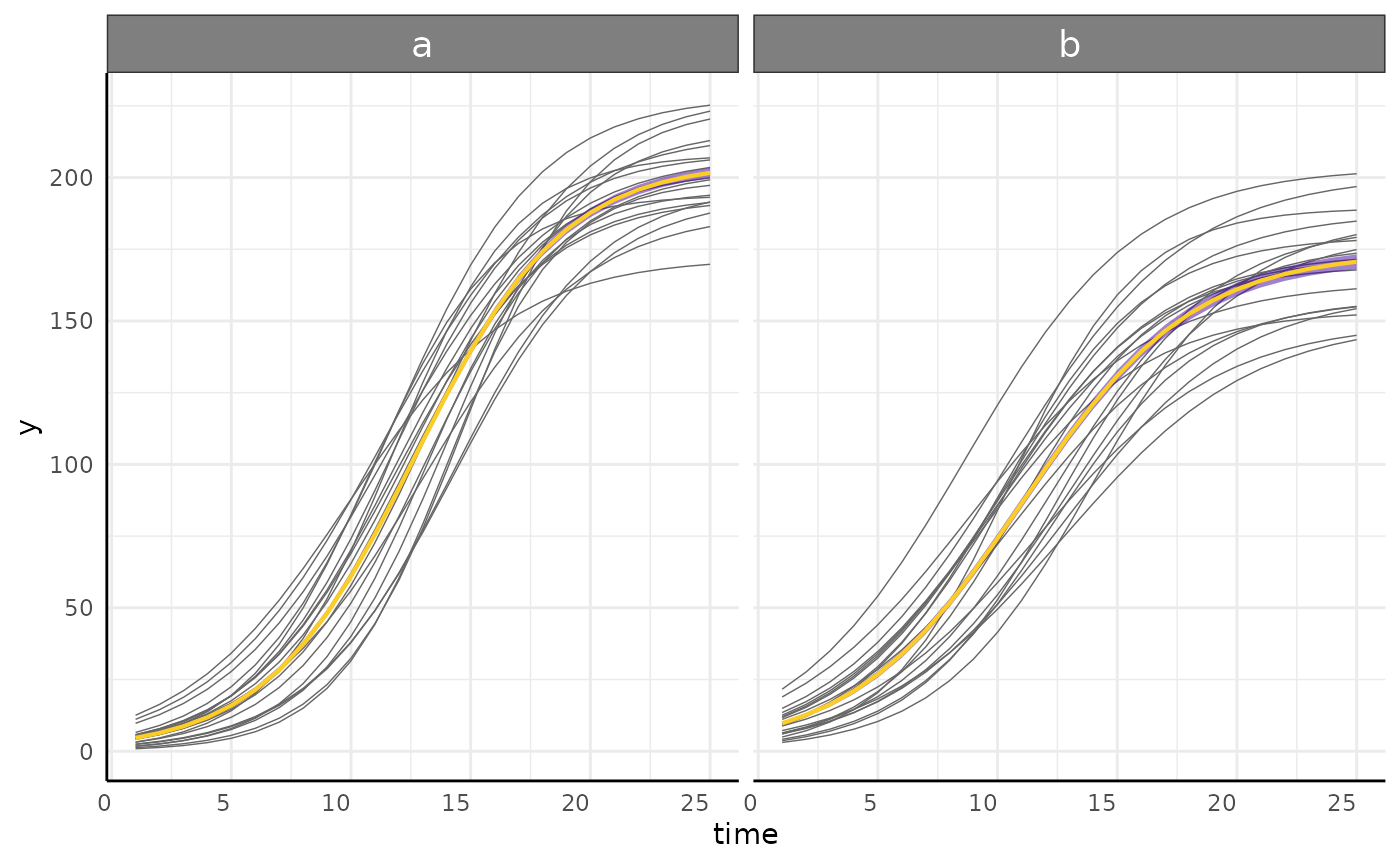
out$plot[[1]] +
  geom_line(
    data = simdf,
    aes(
      x = time, y = y, color = factor(group, levels = c("b", "a")),
      group = paste0(group, id)
    ),
    linewidth = 0.1, show.legend = FALSE
  )

Example of means modeled by splines for two groups.

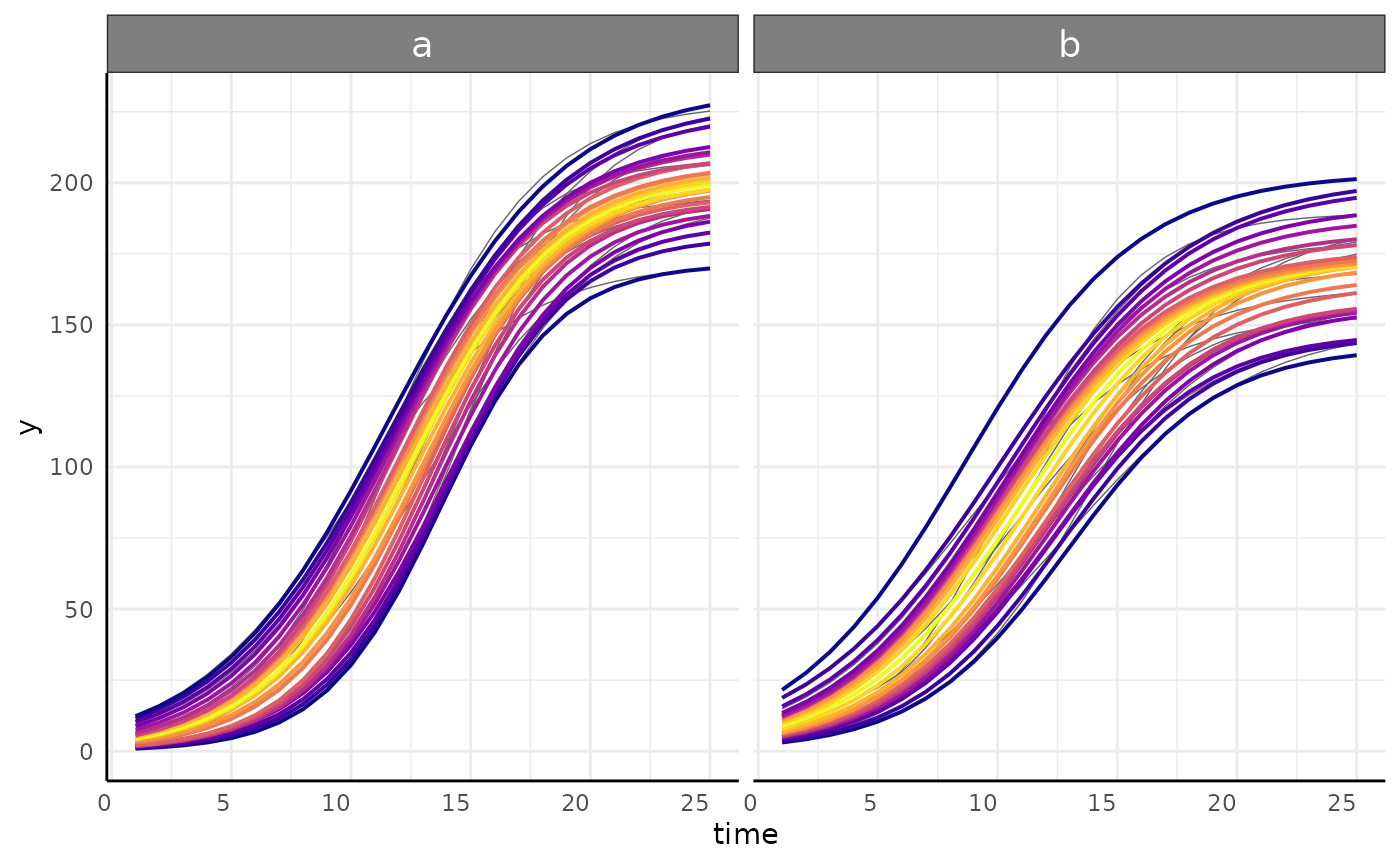
gam_diff differences 

gam_diff(
  model = m, newdata = support, g1 = "a", g2 = "b",
  byVar = "group", smoothVar = "time", plot = TRUE
)$plot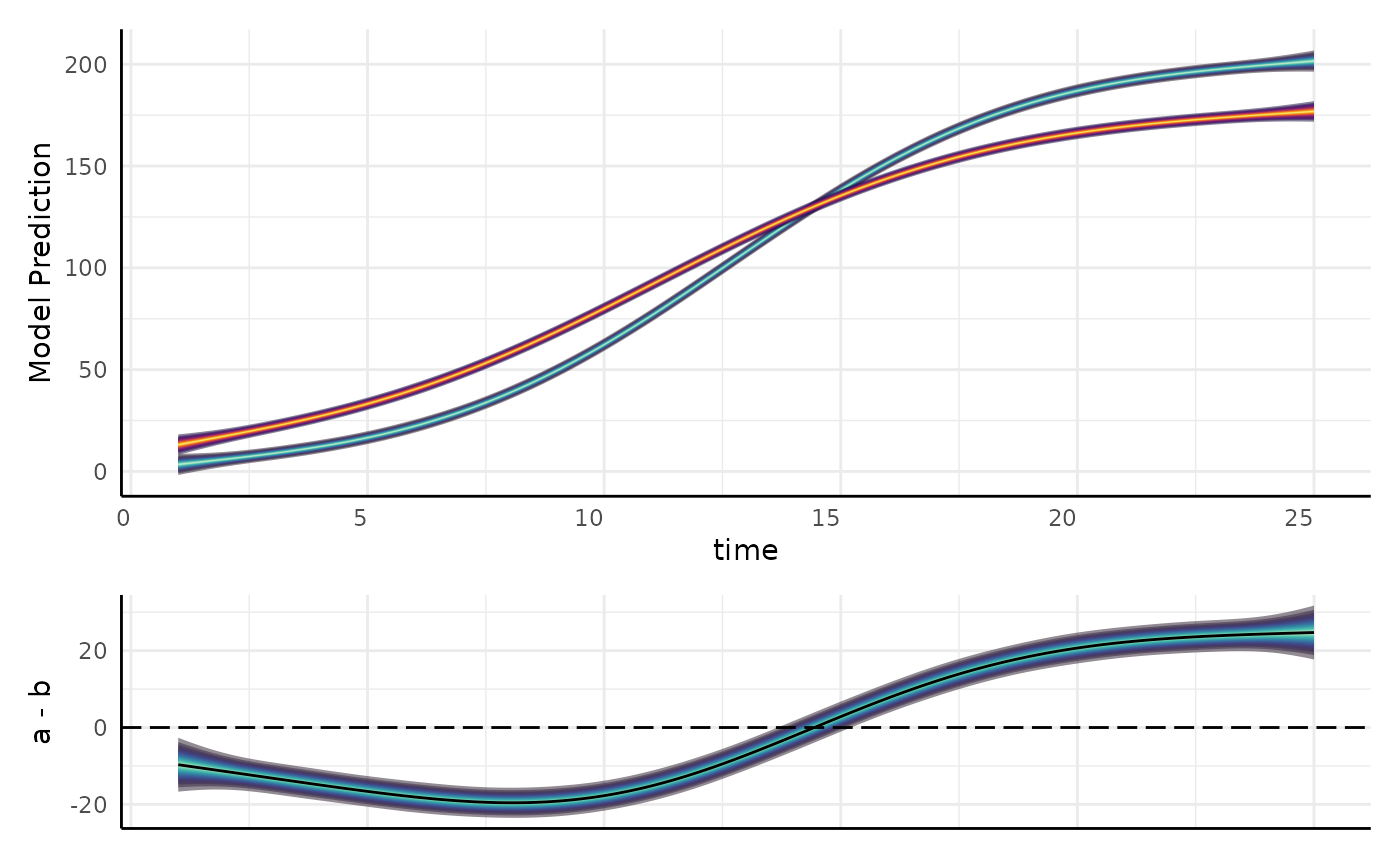

Example of differences between distributions modelled by a spline.

growthSS

Any of these models shown can be specified easily using growthSS.

growthSS - form

With a model specified a rough formula is required to parse your data to fit the model.

The layout of that formula is:

outcome ~ time|individual/group

growthSS - form 2

Here we would use y~time|id/group

head(simdf)
##     id group time         y
## 1 id_1     a    1  6.539088
## 2 id_1     a    2  8.973278
## 3 id_1     a    3 12.263465
## 4 id_1     a    4 16.668316
## 5 id_1     a    5 22.490524
## 6 id_1     a    6 30.057423

growthSS - form 3

We can check that the grouping in our formula is correct with a plot.

ggplot(simdf, aes(
  x = time, y = y,
  group = paste(group, id)
)) +
  geom_line(aes(color = group)) +
  labs(
    title = "Testing Formula",
    subtitle = "y ~ time | id/group"
  ) +
  pcv_theme()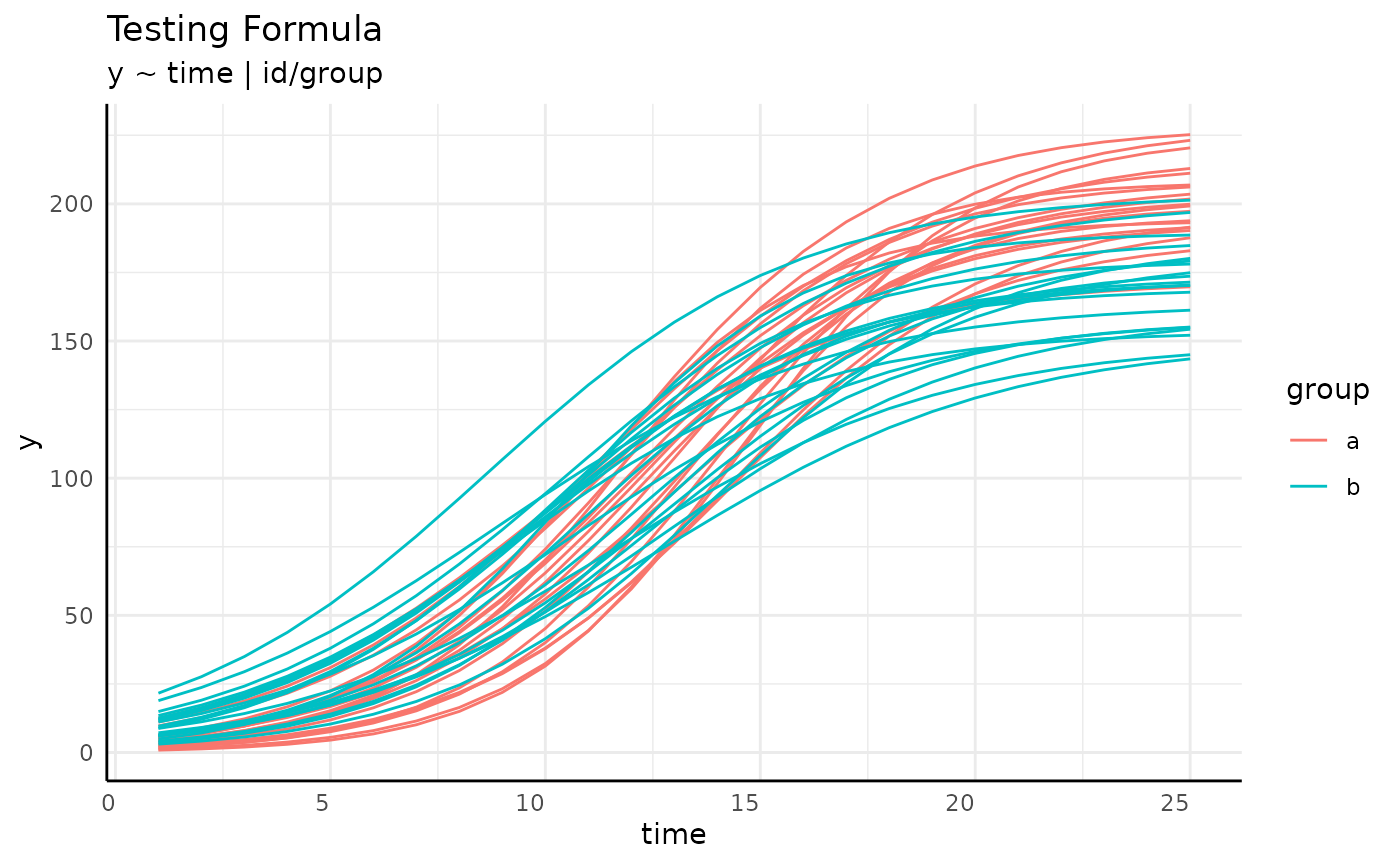

Checking the grouping of data using a ggplot before making a model. We are looking to see that lines follow individual plants over time, here they do.

growthSS - sigma

“nlme” and “brms” models accept a sigma argument. Here we will only look at nlme models as brms models are the subject of the Advanced Growth Modeling tutorial.

growthSS - sigma

Recall the heteroskedasticity problem, shown again with our simulated data:

Example of the homoskedastic assumption failing as standard deviation of the outcome has a non-linear trend.

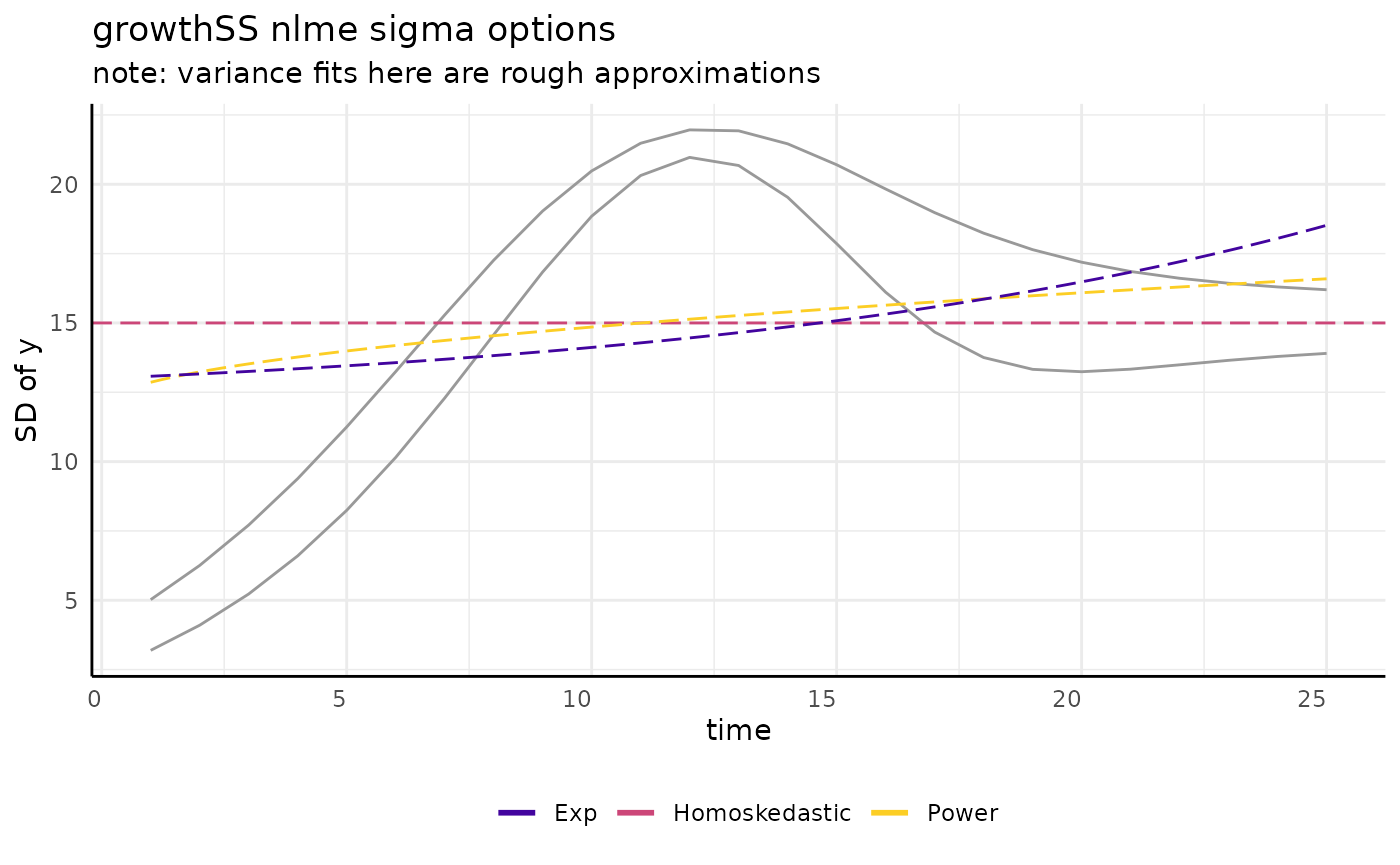
growthSS - sigma

There are lots of ways to model a trend like that we see for sigma.

pcvr offers three options through growthSS for nlme models.

draw_power_sigma <- function(x) {
  return(12 + (x * 0.75)^(2 * 0.26))
} # difficult to recapitulate from nlme
draw_exp_sigma <- function(x) {
  return(12 + exp(2 * x * 0.75 * 0.05))
}

ggplot(sigma_df, aes(x = time, y = y)) +
  geom_line(aes(group = group), color = "gray60") +
  geom_hline(aes(yintercept = 15, color = "Homoskedastic"), linetype = 5, key_glyph = draw_key_path) +
  geom_function(fun = draw_power_sigma, aes(color = "Power"), linetype = 5) +
  geom_function(fun = draw_exp_sigma, aes(color = "Exp"), linetype = 5) +
  scale_color_viridis_d(option = "plasma", begin = 0.1, end = 0.9) +
  guides(color = guide_legend(override.aes = list(linewidth = 1, linetype = 1))) +
  pcv_theme() +
  theme(legend.position = "bottom") +
  labs(
    y = "SD of y", title = "growthSS nlme sigma options", color = "",
    subtitle = "note: variance fits here are rough approximations"
  )

Showing a variety of possible trends for sigma and other distribution parameters to emphasize why any model can be used for any parameter in growthSS

growthSS - “none” sigma

Variance can be modeled as homoskedastic by group.

ggplot(sigma_df, aes(x = time, y = y, group = group)) +
  geom_hline(aes(yintercept = 13.8, color = "Homoskedastic"), linetype = 5, key_glyph = draw_key_path) +
  geom_line(aes(color = group)) +
  scale_color_manual(values = c(scales::hue_pal()(2), "gray40")) +
  pcv_theme() +
  labs(y = "SD of y", color = "Sigma") +
  theme(plot.title = element_blank(), legend.position = "bottom")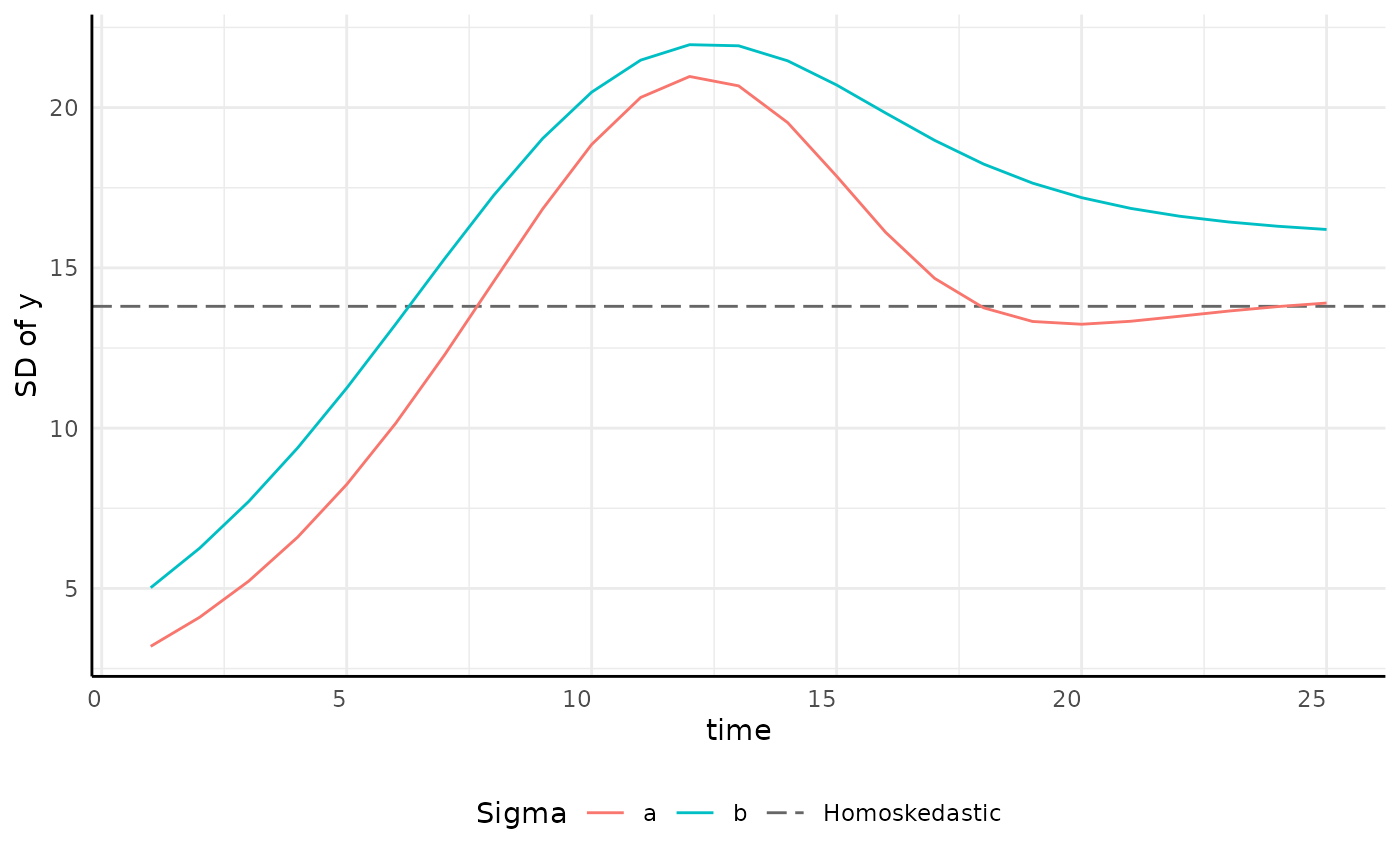

Showing the Homoskedastic assumption and how it can yield a poor fit.

growthSS - “power” sigma

Variance can be modeled using a power of the x term.

ggplot(sigma_df, aes(x = time, y = y, group = group)) +
  geom_function(fun = draw_power_sigma, aes(color = "Power"), linetype = 5) +
  geom_line(aes(color = group)) +
  scale_color_manual(values = c(scales::hue_pal()(2), "gray40")) +
  pcv_theme() +
  labs(y = "SD of y", color = "Sigma") +
  theme(plot.title = element_blank(), legend.position = "bottom")
## Warning: Multiple drawing groups in `geom_function()`
## ℹ Did you use the correct group, colour, or fill aesthetics?

<img src=“/home/runner/work/pcvr/pcvr/docs/articles/pcvrTutorial_igm_files/figure-html/unnamed-chunk-20-1.png” alt=“Showing the”power” option for sigma.” width=“700” />

growthSS - “exp” sigma

Variance can be modeled using a exponent of the x term.

ggplot(sigma_df, aes(x = time, y = y, group = group)) +
  geom_function(fun = draw_exp_sigma, aes(color = "Exp"), linetype = 5) +
  geom_line(aes(color = group)) +
  scale_color_manual(values = c(scales::hue_pal()(2), "gray40")) +
  pcv_theme() +
  labs(y = "SD of y", color = "Sigma") +
  theme(plot.title = element_blank(), legend.position = "bottom")
## Warning: Multiple drawing groups in `geom_function()`
## ℹ Did you use the correct group, colour, or fill aesthetics?

<img src=“/home/runner/work/pcvr/pcvr/docs/articles/pcvrTutorial_igm_files/figure-html/unnamed-chunk-21-1.png” alt=“Showing the”exp” option for sigma.” width=“700” />

growthSS - varFunc Options

nlme varFunc objects can also be passed to the sigma argument in growthSS.

See ?nlme::varClasses for details.

growthSS - start

One of the useful features in growthSS is that you do not need to specify starting values for the supported non-linear models (double sigmoid options notwithstanding).

growthSS - tau

Finally, with mode=“nlrq” the tau argument takes one or more quantiles to fit a model for. By default this is 0.5, corresponding to the median.

growthSS - nls 

nls_ss <- growthSS(
  model = "logistic", form = y ~ time | id / group,
  df = simdf, type = "nls"
)
## Individual is not used with type = 'nls'.
lapply(nls_ss, class)
## $formula
## [1] "formula"
## 
## $start
## [1] "list"
## 
## $df
## [1] "data.frame"
## 
## $pcvrForm
## [1] "formula"
## 
## $type
## [1] "character"
## 
## $model
## [1] "character"
## 
## $call
## [1] "call"

growthSS - nlrq 

nlrq_ss <- growthSS(
  model = "logistic", form = y ~ time | id / group,
  df = simdf, type = "nlrq",
  tau = seq(0.01, 0.99, 0.04)
)
## Individual is not used with type = 'nlrq'.
lapply(nls_ss, class)
## $formula
## [1] "formula"
## 
## $start
## [1] "list"
## 
## $df
## [1] "data.frame"
## 
## $pcvrForm
## [1] "formula"
## 
## $type
## [1] "character"
## 
## $model
## [1] "character"
## 
## $call
## [1] "call"

growthSS - nlme 

nlme_ss <- growthSS(
  model = "logistic", form = y ~ time | id / group,
  df = simdf, sigma = "power", type = "nlme"
)
names(nlme_ss)
## [1] "formula"  "start"    "df"       "pcvrForm" "type"     "model"    "call"
names(nlme_ss$formula)
## [1] "model"    "random"   "fixed"    "groups"   "weights"  "cor_form"

growthSS - mgcv 

mgcv_ss <- growthSS(
  model = "gam", form = y ~ time | id / group,
  df = simdf, type = "mgcv"
)
## Individual is not used with type = 'gam'.
lapply(mgcv_ss, class)
## $formula
## [1] "formula"
## 
## $df
## [1] "data.frame"
## 
## $pcvrForm
## [1] "formula"
## 
## $type
## [1] "character"
## 
## $model
## [1] "character"
## 
## $call
## [1] "call"

growthSS - survival models 

surv_ss <- growthSS(
  model = "survival weibull",
  form = y > 100 ~ time | id / group,
  df = simdf, type = "survreg"
) # type = "flexsurv" has more distribution options
lapply(surv_ss, class)
## $df
## [1] "data.frame"
## 
## $formula
## [1] "formula"
## 
## $pcvrForm
## [1] "formula"
## 
## $distribution
## [1] "character"
## 
## $type
## [1] "character"
## 
## $model
## [1] "character"
## 
## $call
## [1] "call"

growthSS - survival models 

surv_ss <- growthSS(
  model = "survival weibull",
  form = y > 100 ~ time | id / group,
  df = simdf, type = "survreg"
) # type = "flexsurv" has more distribution options
lapply(surv_ss, class)
## $df
## [1] "data.frame"
## 
## $formula
## [1] "formula"
## 
## $pcvrForm
## [1] "formula"
## 
## $distribution
## [1] "character"
## 
## $type
## [1] "character"
## 
## $model
## [1] "character"
## 
## $call
## [1] "call"

Note that here we still supply the standard phenotype data but give a cutoff on the left hand side of the formula. That cutoff represents the “event”. For example, given area in pixels germination might be area_px>10 ~ time|id/group.

fitGrowth

Now that we have the components for our model from growthSS we can fit the model with fitGrowth.

fitGrowth 2

With non-brms models the steps to fit a model specified by growthSS are very simple and can be left to fitGrowth.

nls_fit <- fitGrowth(nls_ss)
nlrq_fit <- fitGrowth(nlrq_ss, cores = 4)
nlme_fit <- fitGrowth(nlme_ss)
mgcv_fit <- fitGrowth(mgcv_ss)
surv_fit <- fitGrowth(surv_ss)

fitGrowth 3

Additional arguments can be passed to fitGrowth and are used as follows:

type …
nls passed to stats::nls
nlrq cores to run in parallel, passed to quantreg::nlrq
nlme passed to nlme::nlmeControl
mgcv passed to mgcv::gam

growthPlot

Models fit by fitGrowth can be visualized using growthPlot.

p_nls <- growthPlot(nls_fit, form = nls_ss$pcvrForm, df = nls_ss$df)
p_nlrq <- growthPlot(nlrq_fit, form = nlrq_ss$pcvrForm, df = nlrq_ss$df)
p_nlme <- growthPlot(nlme_fit, form = nlme_ss$pcvrForm, df = nlme_ss$df)
p_mgcv <- growthPlot(mgcv_fit, form = mgcv_ss$pcvrForm, df = mgcv_ss$df)
p_surv <- growthPlot(surv_fit, form = surv_ss$pcvrForm, df = surv_ss$df)

growthPlot - nls 

p_nls

Showing default plotting for models fit with the nls function.

growthPlot - nlrq 

p_nlrq

Showing default plotting for models fit with the nlrq function.

growthPlot - nlme 

p_nlme

Showing default plotting for models fit with the nlme function.

growthPlot - mgcv 

p_mgcv

Showing default plotting for models fit with the gam function.

growthPlot - surv 

p_surv

Showing default plotting for models fit with the survreg function.

Hypothesis Testing

Hypothesis testing for frequentist non-linear growth models can be somewhat limited.

Broadly, testing is implemented for all backends by comparing models against nested null models and for select backends non-linear testing is available using testGrowth.

testGrowth - nls 

testGrowth(nls_ss, nls_fit, test = "A")$anova
## Analysis of Variance Table
## 
## Model 1: y ~ A/(1 + exp((B[group] - time)/C[group]))
## Model 2: y ~ A[group]/(1 + exp((B[group] - time)/C[group]))
##   Res.Df Res.Sum Sq Df Sum Sq F value    Pr(>F)    
## 1    995     259482                                
## 2    994     235430  1  24052  101.55 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

testGrowth - nls 2 

testGrowth(nls_ss, nls_fit, test = list(
  "A1 - A2",
  "B1 - (B2*1.25)",
  "(C1+1) - C2"
))
##             Form   Estimate        SE   t-value      p-value
## 1        A1 - A2 30.9620463 2.8416998 10.895608 3.418664e-26
## 2 B1 - (B2*1.25) -1.1834444 0.2181014  5.426121 7.235593e-08
## 3    (C1+1) - C2  0.5657608 0.1487875  3.802476 1.519847e-04

testGrowth - nlrq

Here we only print out the comparison for the model of the 49th percentile, but all taus are returned.

testGrowth(nlrq_ss, nlrq_fit, test = "A")[[13]]
## Model 1: y ~ A[group]/(1 + exp((B[group] - time)/C[group]))
## Model 2: y ~ A/(1 + exp((B[group] - time)/C[group]))
##   #Df  LogLik Df  Chisq Pr(>Chisq)    
## 1   6 -4177.2                         
## 2   5 -4228.7 -1 103.02  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

testGrowth - nlme 

testGrowth(nlme_ss, nlme_fit, test = "A")$anova
##         Model df      AIC      BIC    logLik   Test  L.Ratio p-value
## nullMod     1 13 5345.185 5408.986 -2659.593                        
## fit         2 16 5336.665 5415.189 -2652.333 1 vs 2 14.52005  0.0023

testGrowth - nlme 2 

testGrowth(nls_ss, nlme_fit, test = list(
  "A.groupa - A.groupb",
  "B.groupa - (B.groupb*1.25)",
  "(C.groupa+1) - C.groupa"
))
##                         Form  Estimate        SE  Z-value      p-value
## 1        A.groupa - A.groupb 31.406942 4.3866581 7.159651 8.088266e-13
## 2 B.groupa - (B.groupb*1.25) -1.143088 0.2559811 4.465516 7.987592e-06
## 3    (C.groupa+1) - C.groupa  1.000000 0.0000000      Inf 0.000000e+00

testGrowth - mgcv

Due to GAMs nature we cannot test parameters individually.

testGrowth(mgcv_ss, mgcv_fit)$anova
## Analysis of Deviance Table
## 
## Model 1: y ~ s(time)
## Model 2: y ~ 0 + group + s(time, by = group)
##   Resid. Df Resid. Dev     Df Deviance      F    Pr(>F)    
## 1    992.49     315705                                     
## 2    985.48     236017 7.0101    79688 47.572 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

testGrowth - surv

The flexsurv backend provides more flexibility, but standard survreg models are tested using survival::survdiff

testGrowth(surv_ss, surv_fit)
## Call:
## survival::survdiff(formula = ss$formula, data = ss$df)
## 
##          N Observed Expected (O-E)^2/E (O-E)^2/V
## group=a 20       20     20.7    0.0270    0.0939
## group=b 20       20     19.3    0.0291    0.0939
## 
##  Chisq= 0.1  on 1 degrees of freedom, p= 0.8

Final Considerations

  • Pick model builders and parameterizations based on your needs
  • Use GAMs sparingly, they present interpretability problems compared to the parameterized models.
  • Consider the biology behind your observed data while picking a growth model.

Resources

If you run into a novel situation please reach out and we will try to come up with a solution and add it to pcvr if possible.

Good ways to reach out are the help-datascience slack channel and pcvr github repository.