Skip to contents

Helper function for visualizing differences in GAMs fit with mgcv::gam

Source: R/gam_helpers.R
gam_diff.Rd

Note that using GAMs will be less useful than fitting parameterized models as supported by growthSS and fitGrowth for common applications in plant phenotyping.

Usage

gam_diff(
  model,
  newdata = NULL,
  g1,
  g2,
  byVar = NULL,
  smoothVar = NULL,
  cis = seq(0.05, 0.95, 0.05),
  unconditional = TRUE,
  plot = TRUE
)

Arguments

model

A model fit with smooth terms by mgcv::gam

newdata

A data.frame of new data to use to make predictions. If this is left NULL (the default) then an attempt is made to make newdata using the first smooth term in the formula. See examples for guidance on making appropriate newdata

g1

A character string for the level of byVar to use as the first group to compare, if plot=TRUE then this will be shown in blue.

g2

The second group to compare (comparison will be g1 - g2). If plot=TRUE then this will be shown in red.

byVar

Categorical variable name used to separate splines as a string.

smoothVar

The variable that splines were used on. This will often be a time variable.

cis

Confidence interval levels, can be multiple. For example, 0.95 would return Q_0.025 and Q_0.975 columns, and c(0.9, 0.95) would return Q_0.025, Q_0.05, Q_0.95, and Q_0.975 columns. Defaults to seq(0.05, 0.95, 0.05)

unconditional

Logical, should unconditional variance-covariance be used in calculating standard errors. Defaults to TRUE.

plot

Logical, should a plot of the difference be returned? Defaults to TRUE.

Value

A dataframe or a list containing a ggplot and a dataframe

Examples


ex <- pcvr::growthSim("logistic",
  n = 20, t = 25,
  params = list(
    "A" = c(200, 160),
    "B" = c(13, 11),
    "C" = c(3, 3.5)
  )
)

m <- mgcv::gam(y ~ group + s(time, by = factor(group)), data = ex)

support <- expand.grid(
  time = seq(min(ex$time), max(ex$time), length = 400),
  group = factor(unique(ex$group))
)

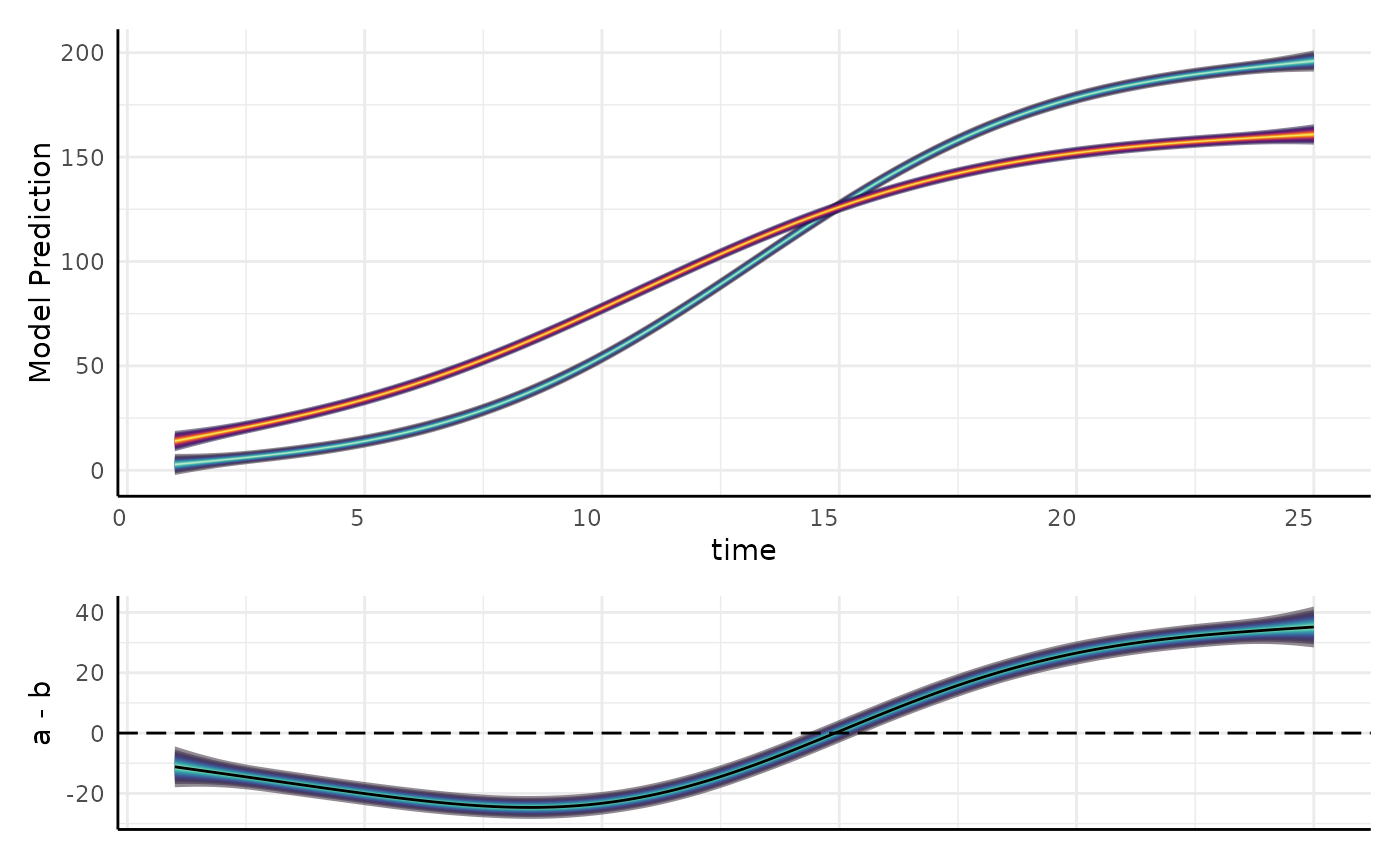
out <- gam_diff(
  model = m, newdata = support, g1 = "a", g2 = "b",
  byVar = "group", smoothVar = "time", plot = TRUE
)
dim(out$data)
#> [1] 400 120
out$plot

out2 <- gam_diff(
  model = m, g1 = "a", g2 = "b", byVar = NULL, smoothVar = NULL, plot = TRUE
)