Bellwether

Josh Sumner, DDPSC Data Science Core Facility

2023-10-16

.static-code {
  background-color: white;
  border: 1px solid lightgray;
}
.simulated {
  background-color: #EEF8FB;
  border: 1px solid #287C94;
}

library(pcvr)
library(data.table) # for fread
library(ggplot2)
library(patchwork) # for easy ggplot manipulation/combination

Example Bellwether (Lemnatech) Workflow

The Bellwether phenotyping facility at the Donald Danforth Plant Science Center allows for high throughput image based phenotyping of up to 1140 plants over the course of several weeks. This generates a massive amount of image data which is typically analysed using plantCV, a python based image analysis tool developed and maintained by the Data Science Core Facility at DDPSC. The plantCV output from a Bellwether experiment consists of numeric phenotypes commonly broken into two categories, single value traits and multi value traits. Single value traits are phenotypes where one image yields one value, things like plant height or plant area. Multi value traits require multiple numbers to describe a single image and currently are limited to color histograms in various color spaces. Here we will focus only on the hue channel of HSV color, but there are lots of options with your data. This package is being developed to help with common analysis tasks that arise in using plantCV output. If your goal or experiment seems to be unsupported then please consider raising an issue on github so we can know what directions to take development in for the future.

Installation of pcvr from github is possible with the remotes or devtools packages. You may need to restart R after installing or reinstalling packages.

devtools::install_github("joshqsumner/pcvr", build_vignettes = TRUE)
library(pcvr)

If you clone that repository and are making edits then you can easily use your local version with: devtools::load_all("file/path/to/local/pcvr")

Functions in pcvr use colorblind friendly palettes from the viridis package if they specify color/fill scales. Some functions do not specify a color/fill scale and use ggplot2 defaults. If you use these functions or base work off of them please be mindful of your choices regarding color.

As a final note before starting into pcvr, this vignette is laid out to help guide analyses from Bellwether experiments these functions tend to be generalizable and can be used for other plantCV data as well. There are some code chunks in this vignette that you are only presented to demonstrate syntax and that you are not meant to run locally if following along. Those are identified by style:

complicatedFunction("syntax") # do not run this style

1 + 1 # run this style

## [1] 2

support <- seq(0, 1, 0.0001) # this style is simulated data
plot(support, dbeta(support, 5, 5), type = "l", main = "simulated example")

Load Data

In this vignette we will use simulated data but there are examples on github using PlantCV output read from online if you run into metadata handling problems. This simulated data picks up roughly where the Reading pcv data article ends.

set.seed(123)
d <- growthSim("logistic",
  n = 30, t = 25,
  params = list(
    "A" = c(140, 155, 150, 165, 180, 190, 175, 185, 200, 220, 210, 205),
    "B" = c(13, 11, 12, 11, 10, 11, 12, 13, 14, 12, 12, 13),
    "C" = c(3, 3.25, 3.5, 3.1, 2.9, 3.4, 3.75, 2.9, 3, 3.1, 3.25, 3.3)
  )
)
d$genotype <- ifelse(d$group %in% letters[1:3], "MM",
  ifelse(d$group %in% letters[4:6], "B73",
    ifelse(d$group %in% letters[7:9], "Mo17", "W605S")
  )
)
d$fertilizer <- ifelse(d$group %in% letters[seq(1, 12, 3)], 0,
  ifelse(d$group %in% letters[seq(2, 12, 3)], 50, 100)
)
colnames(d)[c(1, 3, 4)] <- c("barcode", "DAS", "area_cm2")
d$height_cm <- growthSim("monomolecular",
  n = 30, t = 25,
  params = list(
    "A" = c(
      25, 30, 35, 32, 34, 30,
      37, 36, 34, 33, 35, 38
    ),
    "B" = c(
      0.12, 0.08, 0.1, 0.11, 0.1,
      0.12, 0.07, 0.12, 0.11, 0.09, 0.08, 0.09
    )
  )
)$y
d$width_cm <- growthSim("power law",
  n = 30, t = 25,
  params = list(
    "A" = c(
      10, 14, 13, 11, 12, 13,
      10, 13, 14, 11, 14, 14
    ),
    "B" = c(
      1.05, 1.13, 1.17, 1.01, 1.2,
      1, 1.04, 1.07, 1.17, 1.04, 1.16, 1.17
    )
  )
)$y
d$hue_circular_mean_degrees <- growthSim("linear",
  n = 30, t = 25,
  params = list("A" = c(runif(12, 1, 3)))
)$y +
  round(runif(nrow(d), 50, 60))
sv_ag <- d

FREM

Now that our data is read in and has undergone some basic quality control we want to know which phenotypes are best explained by our design variables. The frem function partitions variance using a fully random effects model (frem). Here we provide our dataframe, the design variables, the phenotypes, and the column representing time. By default frem will use the last timepoint, but this is controlled with the time argument. For this first example we mark the singular model fits (markSingular=TRUE) to indicate places where lme4::lmer had some convergence issues. Generally these issues are minor and do not cause problems for interpreting these models, but you can pass additional arguments to lme4::lmer through additional arguments if desired.

frem(sv_ag,
  des = c("genotype", "fertilizer"),
  phenotypes = c("area_cm2", "height_cm", "width_cm", "hue_circular_mean_degrees"),
  timeCol = "DAS", cor = TRUE, returnData = FALSE, combine = FALSE, markSingular = TRUE, time = NULL
)

## [[1]]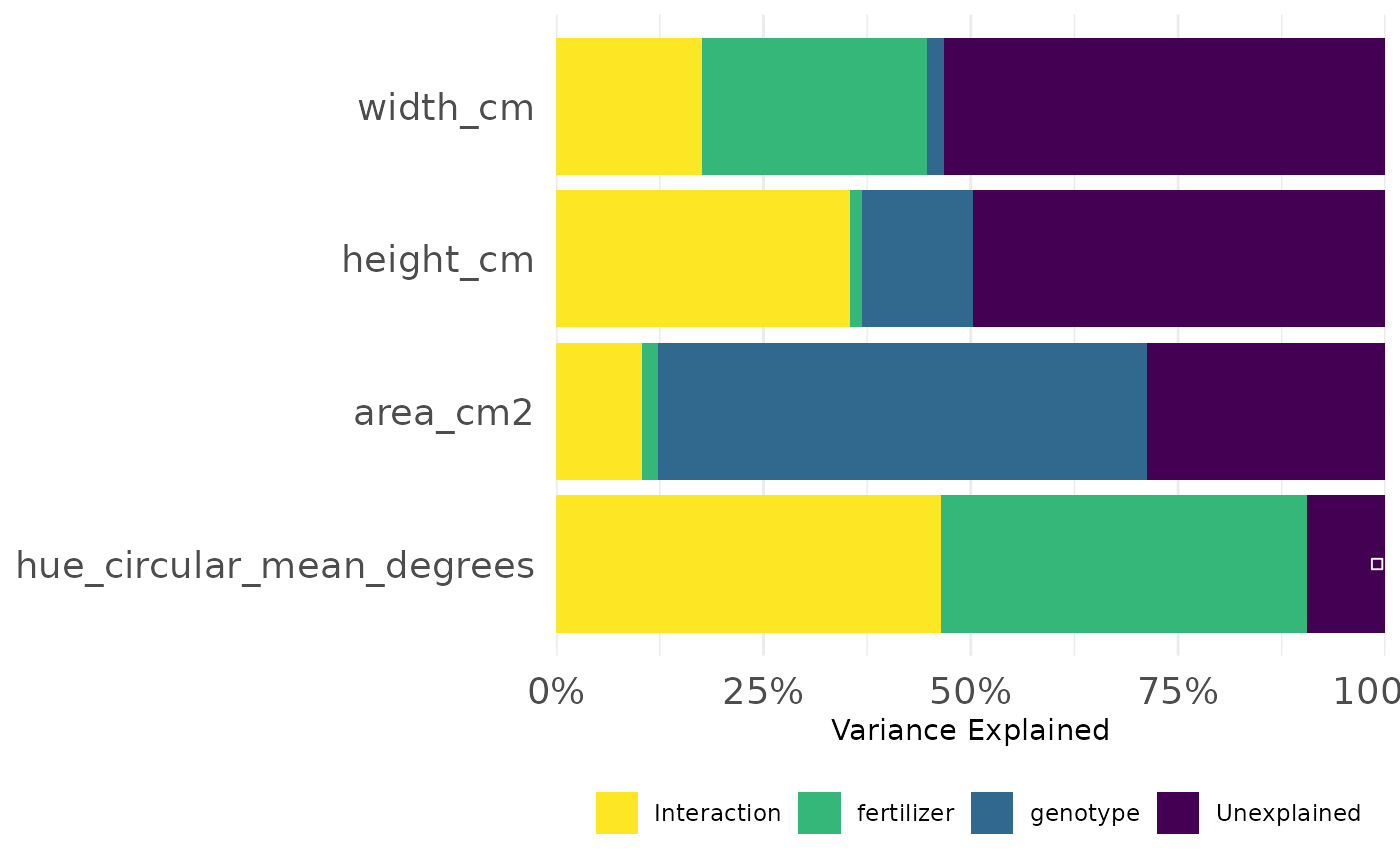

## 
## [[2]]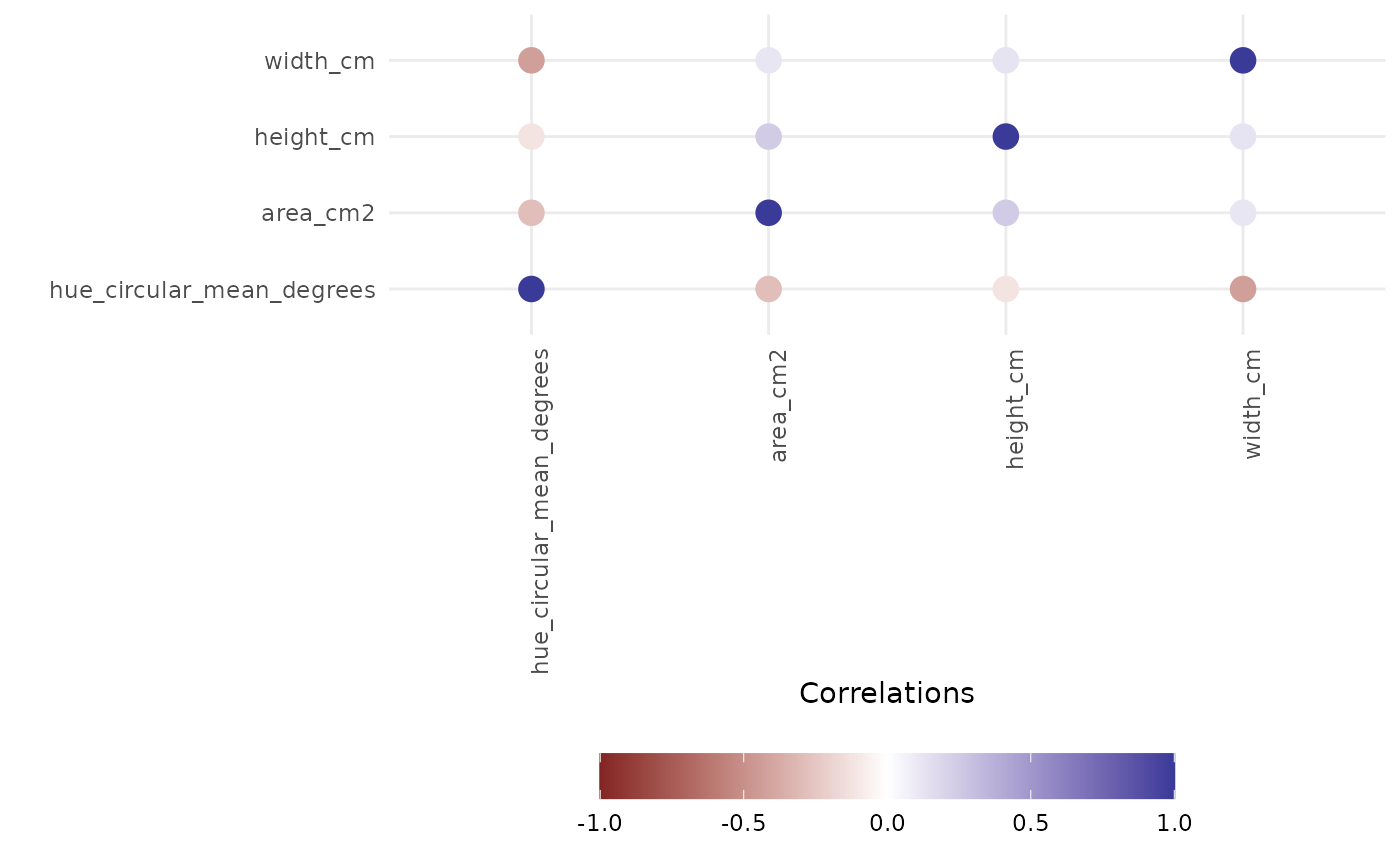

Here we look at how much variance in each phenotype was explained over the course of the experiment. We could also specify a set of times (time = c(10:14) for example) if we are most interested in a particular timeframe.

frem(sv_ag,
  des = c("genotype", "fertilizer"),
  phenotypes = c("area_cm2", "height_cm", "width_cm"),
  timeCol = "DAS", cor = FALSE, returnData = FALSE, combine = FALSE, markSingular = FALSE, time = "all"
)

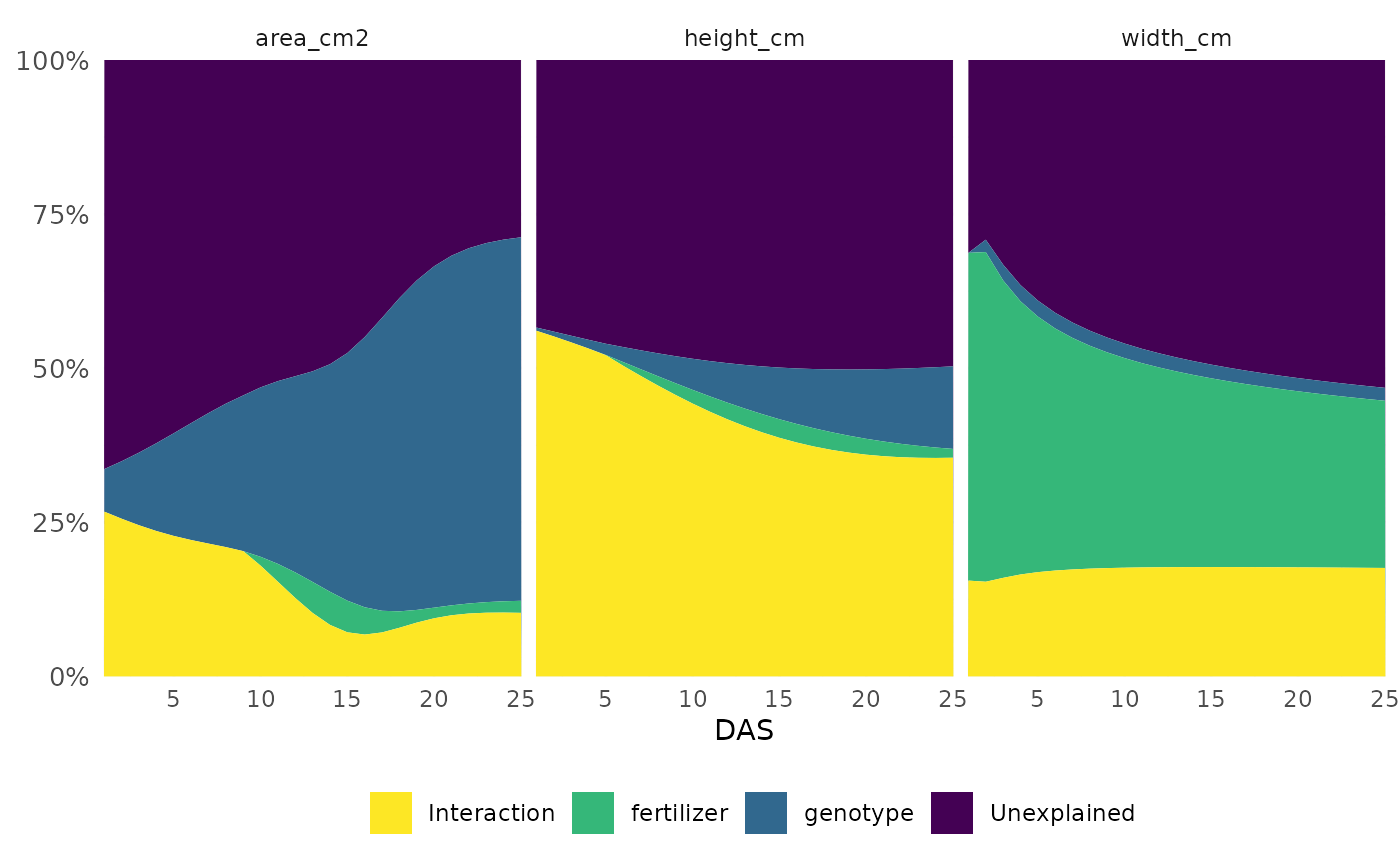
This informs our next steps. Hue and size based phenotypes are well explained by our design variables so we might decide to focus more complex analyses on those. In this experiment mini maize is one of the genotypes and the fertilizer treatment has an option with no nitrogen, so this intuitively makes sense and passes an eye check.

Single Value Traits

Most analysis focus on single value traits, that is phenotypes where one object in an image returns on numeric value such as area or height. These can be compared longitudinally or with respect to individual days. Note that we do not recommend using a PCA of the single value traits to look for differences in your treatment groups, these traits are interpretable on their own and are interdependent enough that a PCA is not appropriate.

Growth Trendlines

Trendlines help us decide what next steps make the most sense and give a general impression of which conditions yielded healthier plants.

ggplot(sv_ag, aes(
  x = DAS, y = area_cm2, group = interaction(genotype, fertilizer, lex.order = TRUE),
  color = genotype
)) +
  facet_wrap(~ factor(fertilizer, levels = c("0", "50", "100"))) +
  geom_smooth(method = "loess", se = TRUE, fill = "gray90") +
  geom_line(aes(group = barcode), linewidth = 0.15) +
  labs(
    y = expression("Area" ~ "(cm"^2 ~ ")"),
    color = "Genotype"
  ) +
  guides(color = guide_legend(override.aes = list(linewidth = 5))) +
  pcv_theme() +
  theme(axis.text.x.bottom = element_text(angle = 0))

## `geom_smooth()` using formula = 'y ~ x'

Single day comparisons

Non-longitudinal data (or single day data from larger longitudinal data) can be compared using the conjugate function. conjugate uses conjugate priors to make simple Bayesian comparisons for several types of data. Optionally, region of practical equivalence (ROPE) testing is also supported. Most distirubtions supported by this function can be used with either wide or long single value data or wide multi-value data. See ?pcvr::conjugate or the conjugate tutorial for details on usage and available options.

mo17_area <- sv_ag[sv_ag$genotype == "Mo17" & sv_ag$DAS > 18 & sv_ag$fertilizer == 100, "area_cm2"]
b73_area <- sv_ag[sv_ag$genotype == "B73" & sv_ag$DAS > 18 & sv_ag$fertilizer == 100, "area_cm2"]

area_res_t <- conjugate(s1 = mo17_area, s2 = b73_area, method = "t", plot = TRUE, rope_range = c(-5, 5))

Here we can see a dramatic difference in our posterior distributions between genotypes and the distribution of differences between these samples is entirely outside of our ROPE range.

Relative Tolerance

Often bellwether experiments involve comparing stress tolerance between groups. For example in this dataset we might want to know which genotype shows the most resilience to reduced fertilizer. To easily check this we can change out data with relativeTolerance. Details on this function can be read with ?pcvr::relativeTolerance. Note that if you are going to be making a longitudinal model anyway then it makes more sense to use the model to assess relative tolerance rather than transforming data into a different unit.

rt <- relativeTolerance(sv_ag,
  phenotypes = c("area_cm2", "height_cm"),
  grouping = c("fertilizer", "genotype", "DAS"), control = "fertilizer", controlGroup = "100"
)

ggplot(
  rt[rt$phenotype == "area_cm2" & rt$DAS %in% c(10:12), ],
  aes(x = DAS, y = mu_rel, fill = interaction(fertilizer, genotype))
) +
  geom_col(position = "dodge") +
  geom_errorbar(aes(ymin = mu_rel - 1.96 * se_rel, ymax = mu_rel + 1.96 * se_rel),
    position = position_dodge(width = 0.9), width = 0.3
  ) +
  pcv_theme() +
  labs(y = "Relative Tolerance", fill = "Fertilizer\nand Genotype")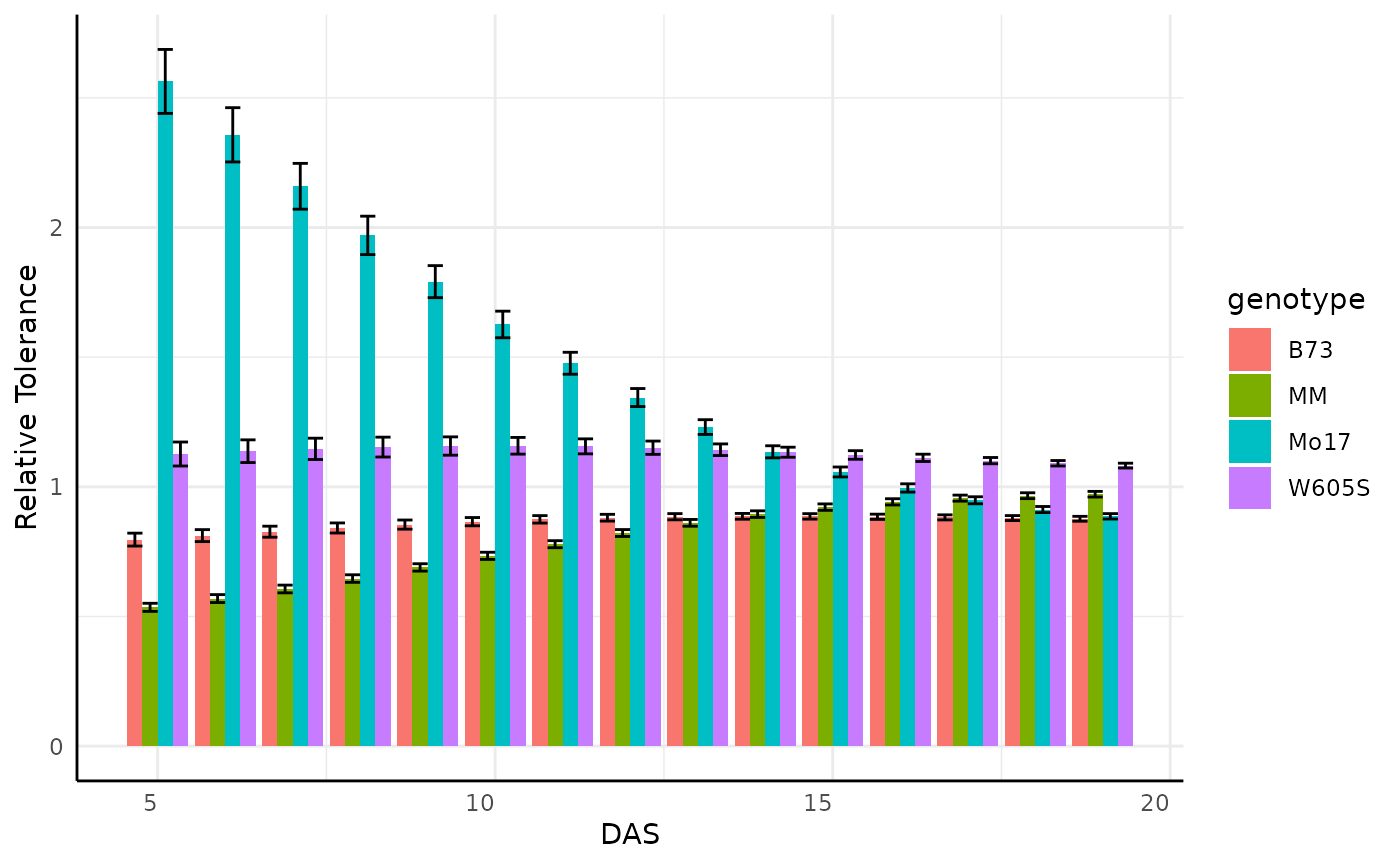

Looking at the entire data for the area phenotype is very busy so we might subset to look at something more specific, where we see some odd products of the plants germinating on the bellwether system.

pd <- rt[rt$phenotype == "area_cm2" & rt$DAS %in% c(5:19) & rt$fertilizer == "0", ]
pd$upper_2se <- pd$mu_rel + 2 * pd$se_rel
pd$lower_2se <- pd$mu_rel - 2 * pd$se_rel

ggplot(pd, aes(x = DAS, y = mu_rel, fill = genotype)) +
  geom_col(position = "dodge") +
  geom_errorbar(aes(
    ymin = lower_2se, ymax = upper_2se,
    group = genotype
  ), position = "dodge") +
  pcv_theme() +
  labs(y = "Relative Tolerance")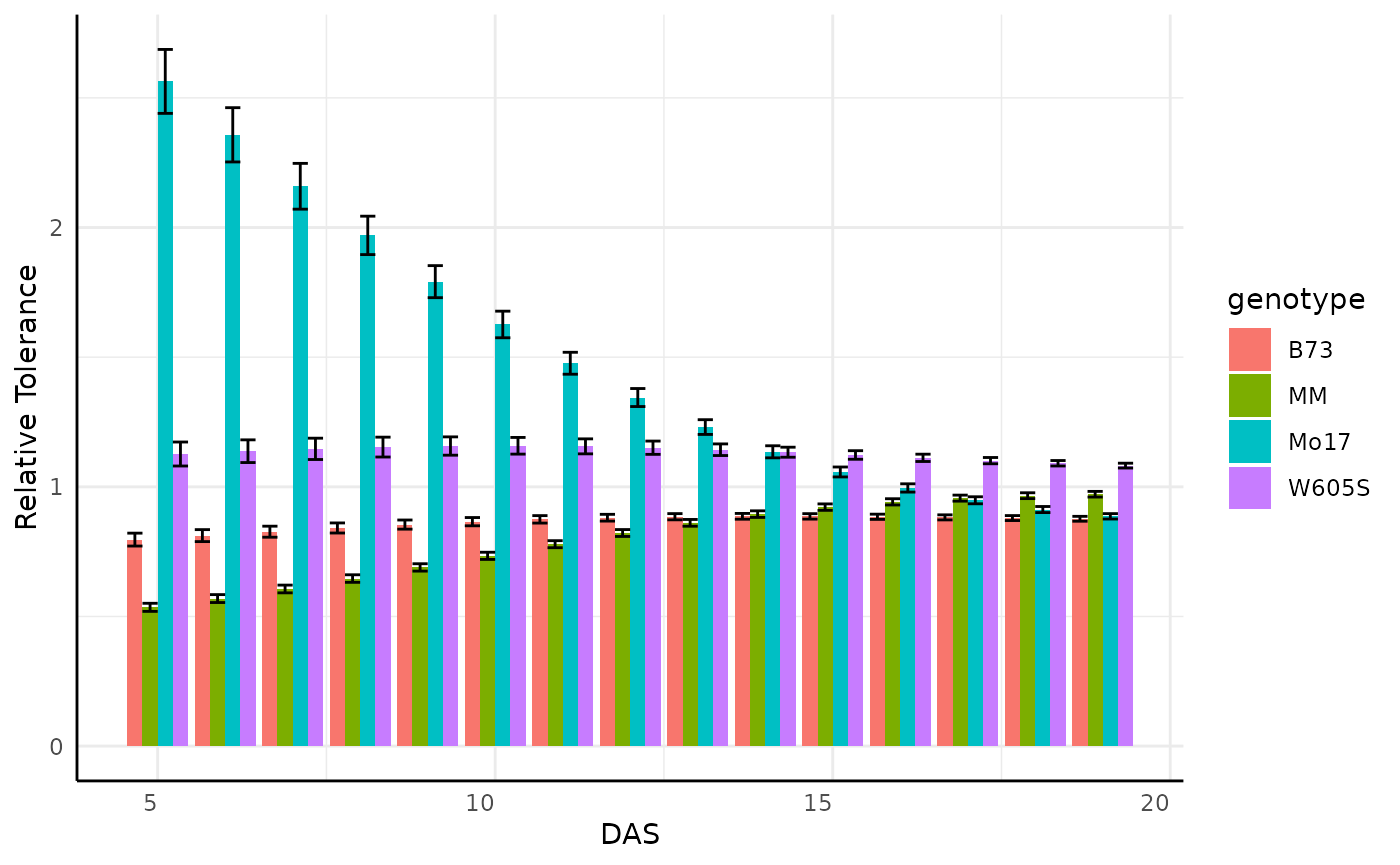

Cumulative Phenotypes

Sometimes we might want to use the cumulative difference over time

cp <- cumulativePheno(sv_ag, phenotypes = c("area_cm2", "height_cm"), group = "barcode", timeCol = "DAS")

We can check that this worked correctly with trendlines:

ggplot(cp, aes(x = DAS, y = area_cm2_csum, color = genotype, group = barcode)) +
  facet_wrap(~ factor(fertilizer, levels = c("0", "50", "100"))) +
  geom_line() +
  pcv_theme() +
  labs(
    y = expression("Cumulative Sum of Area" ~ "(cm"^2 ~ ")"),
    color = "Genotype"
  )

Longitudinal Modeling

Longitudinal modeling is the most comprehensive way to use the single value traits from a bellwether experiment. Longitudinal modeling can also be complicated compared to single timepoint analyses. Statistical complications including changes in variance, non-linearity, and autocorrelation present potential problems in analyses. To address these we recommend using hierarchical models. pcvr attempts to lower the barrier to entry for these models with helper functions for use with brms, nlme, nlrq, mgcv, and nls. Here we focus only on brms models, but there are tutorials that cover more options.

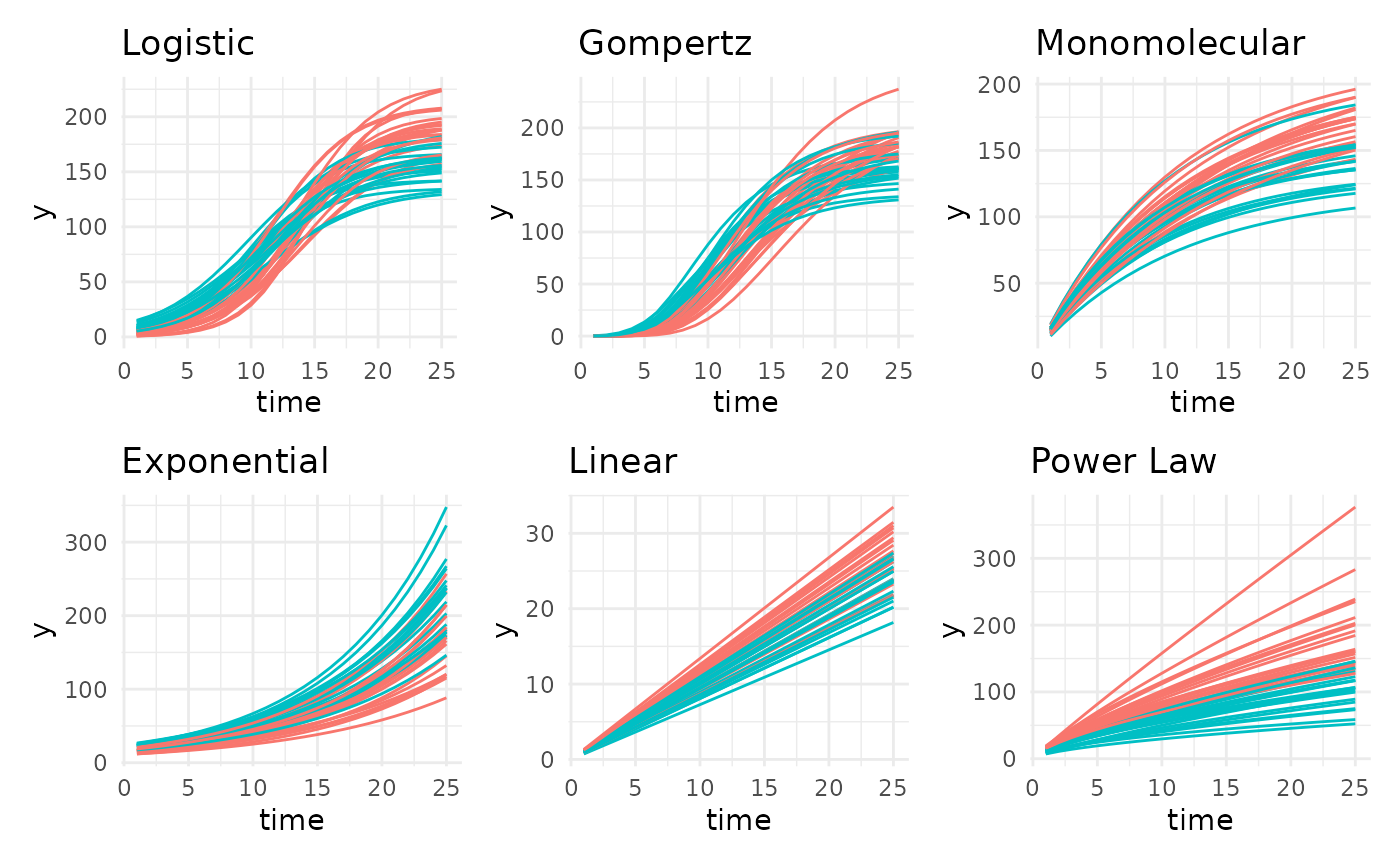
Growth Model Forms

Based on literature and observed trends there are 13 growth models that pcvr supports. The six most common of those are shown here using the growthSim function but the remaining options could be visualized in the same way.

simdf <- growthSim("logistic",
  n = 20, t = 25,
  params = list("A" = c(200, 160), "B" = c(13, 11), "C" = c(3, 3.5))
)
l <- ggplot(simdf, aes(time, y, group = interaction(group, id))) +
  geom_line(aes(color = group)) +
  labs(title = "Logistic") +
  theme_minimal() +
  theme(legend.position = "none")

simdf <- growthSim("gompertz",
  n = 20, t = 25,
  params = list("A" = c(200, 160), "B" = c(13, 11), "C" = c(0.2, 0.25))
)
g <- ggplot(simdf, aes(time, y, group = interaction(group, id))) +
  geom_line(aes(color = group)) +
  labs(title = "Gompertz") +
  theme_minimal() +
  theme(legend.position = "none")

simdf <- growthSim("monomolecular",
  n = 20, t = 25,
  params = list("A" = c(200, 160), "B" = c(0.08, 0.1))
)
m <- ggplot(simdf, aes(time, y, group = interaction(group, id))) +
  geom_line(aes(color = group)) +
  labs(title = "Monomolecular") +
  theme_minimal() +
  theme(legend.position = "none")

simdf <- growthSim("exponential",
  n = 20, t = 25,
  params = list("A" = c(15, 20), "B" = c(0.095, 0.095))
)
e <- ggplot(simdf, aes(time, y, group = interaction(group, id))) +
  geom_line(aes(color = group)) +
  labs(title = "Exponential") +
  theme_minimal() +
  theme(legend.position = "none")

simdf <- growthSim("linear", n = 20, t = 25, params = list("A" = c(1.1, 0.95)))
ln <- ggplot(simdf, aes(time, y, group = interaction(group, id))) +
  geom_line(aes(color = group)) +
  labs(title = "Linear") +
  theme_minimal() +
  theme(legend.position = "none")

simdf <- growthSim("power law", n = 20, t = 25, params = list("A" = c(16, 11), "B" = c(0.75, 0.7)))
pl <- ggplot(simdf, aes(time, y, group = interaction(group, id))) +
  geom_line(aes(color = group)) +
  labs(title = "Power Law") +
  theme_minimal() +
  theme(legend.position = "none")

(l + g + m) / (e + ln + pl)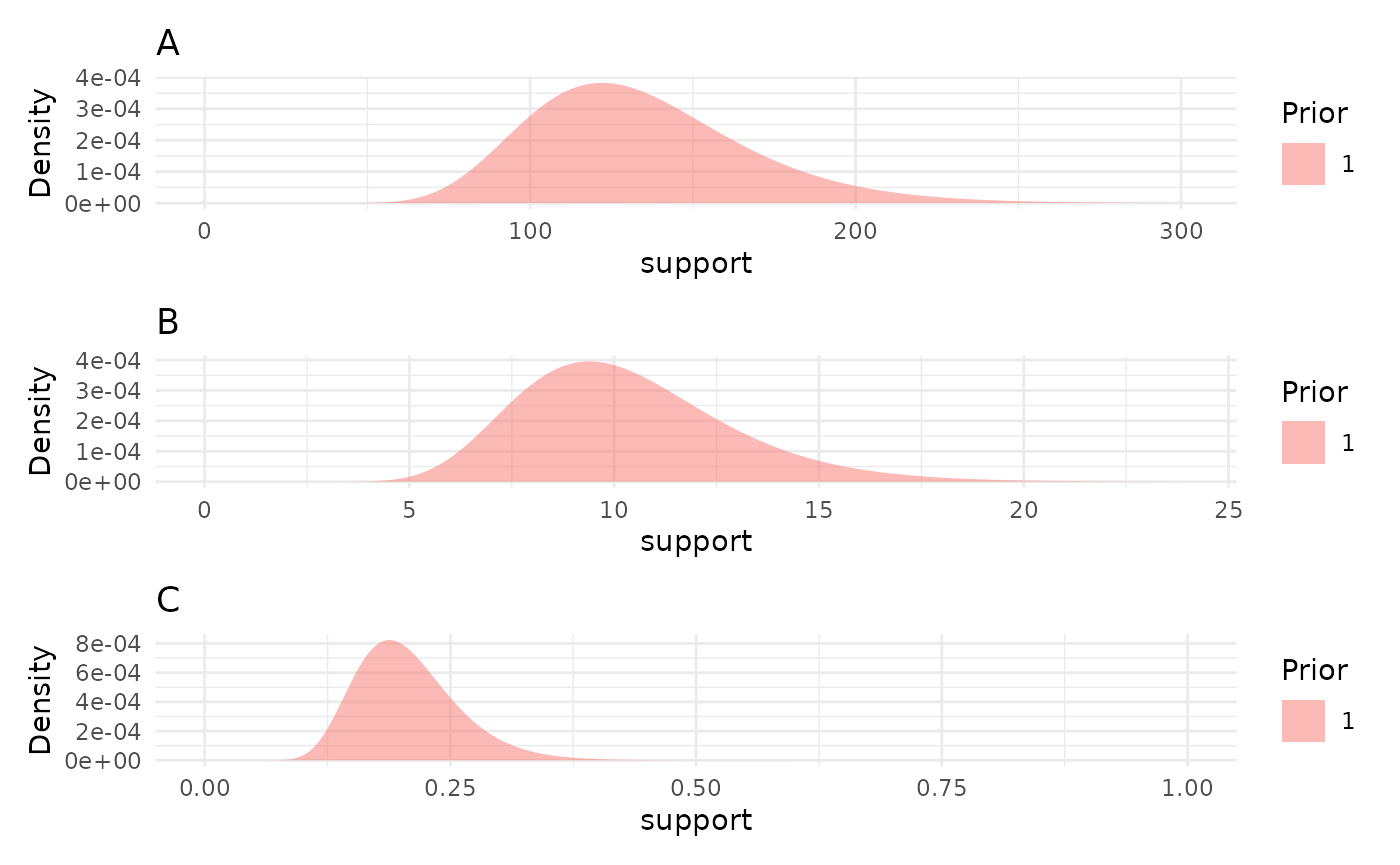

Typically at least one of these models will be a good fit to your bellwether data, with gompertz models being the most broadly useful so far. In this experiment the plants were not germinated before being added to the machine, so we might not see asymptotic size. Still, conceptually we know that these plants will stop growing in the near future so we might use a gompertz model in place of the exponential model that looks most like our loess trendlines.

Model setup

Coding a multilevel Bayesian model can be a difficult and time consuming process. Even with the greatly simplified syntax used by brms this can present a barrier to entry for some people who could benefit from using very robust models. To help get around this potential issue for the specific case of measuring growth over time pcvr includes several functions to work with brms, the first of which is growthSS, a self-starter helper function for use with brms::brm.

submodel options

For the purposes of this vignette we will only consider the default Student T model family, for examples of other model families (useful for count or circular data especially) see the Advanced Growth Modeling tutorial on github or the longitudinal growth vignette.

There are several ways to consider variance over time. By default almost all modeling assumes homoscedasticity, that is constant variance across predictor variables (time here). That assumption is very unrealistic in biological settings since all seeds/seedlings will start from a very low area but will grow differently through the experiment. The growthSS function can use any of the main growth model options as a model for distributional parameters (here being sigma). Splines or asymptotic models will often yield the best fit to your data’s variance.

Prior Distributions

An important part of Bayesian statistics is setting an appropriate prior. These represent your knowledge about the field and are used along with your collected data to yield results. Priors should generally be weak relative to your data, meaning that if your prior belief is wrong then your experiment can move the posterior distribution away from the prior in a meaningful way.

In growthSS priors can be specified as a brmsprior object (in which case it is used as is), a named list (names representing parameters), or a numeric vector, where values will be used to generate lognormal priors with a long right tail. Lognormal priors with long right tails are used because the values for our growth curves are strictly positive and the lognormal distribution is easily interpreted. The tail is a product of the variance, which is assumed to be 0.25 for simplicity and to ensure priors are wide. This means that only a location parameter needs to be provided. If a list is used then each element of the list can be length 1 in which case each group will use the same prior or it can be a vector of the same length as unique(data$group) where group is your grouping variable from the form argument to growthSS. If a vector is used then a warning will be printed to check that the assumed order of groups is correct. The growthSim function can be useful in thinking about what a reasonable prior distribution might be, although priors should not be picked by trying to get a great fit by eye to your collected data.

We can check the priors made by growthSS with the plotPrior function, which can take a list of priors or the growthSS output.

priors <- list("A" = 130, "B" = 10, "C" = 0.2)
priorPlots <- plotPrior(priors)
priorPlots[[1]] / priorPlots[[2]] / priorPlots[[3]]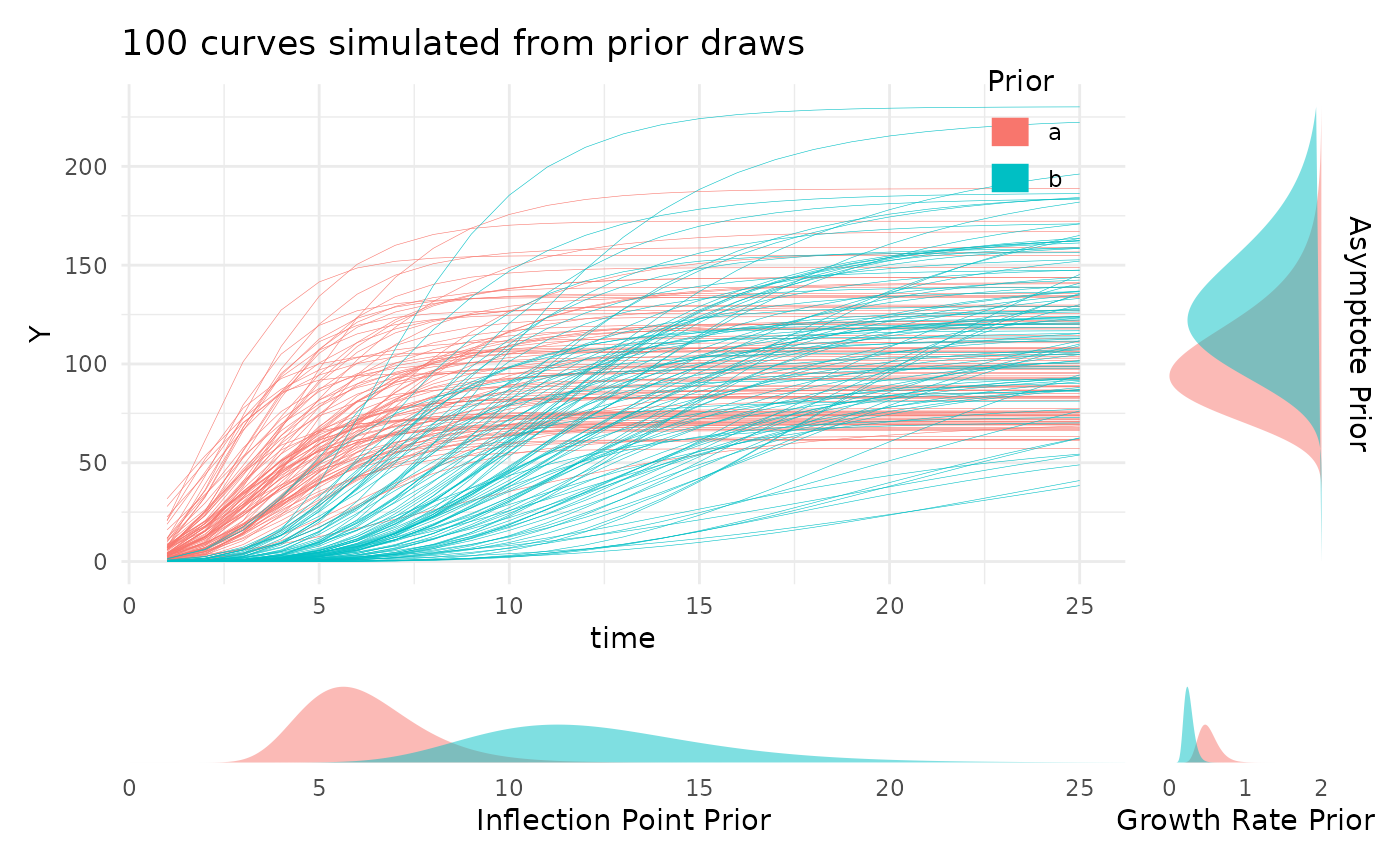

Looking at the prior distributions this way is useful, but for those still familiarizing with a given growth model the parameter values may not be very intuitive. To help with picking reasonable priors while familiarizing with the meaning of the model parameters the plotPrior function can also simulate growth curves by making draws from the specified prior distributions. Here is an example of using plotPrior in this way to pick between possible sets of prior distributions for a gompertz model. For asymptotic distributions the prior on “A” is added to the y margin. For distributions with an inflection point the prior on “B” is shown in the x margin. Arbitrary numbers of priors can be compared in this manner, but more than two or three can be cluttered so an iterative process is recommended if you are learning about your growth model.

twoPriors <- list("A" = c(100, 130), "B" = c(6, 12), "C" = c(0.5, 0.25))
plotPrior(twoPriors, "gompertz", n = 100)[[1]]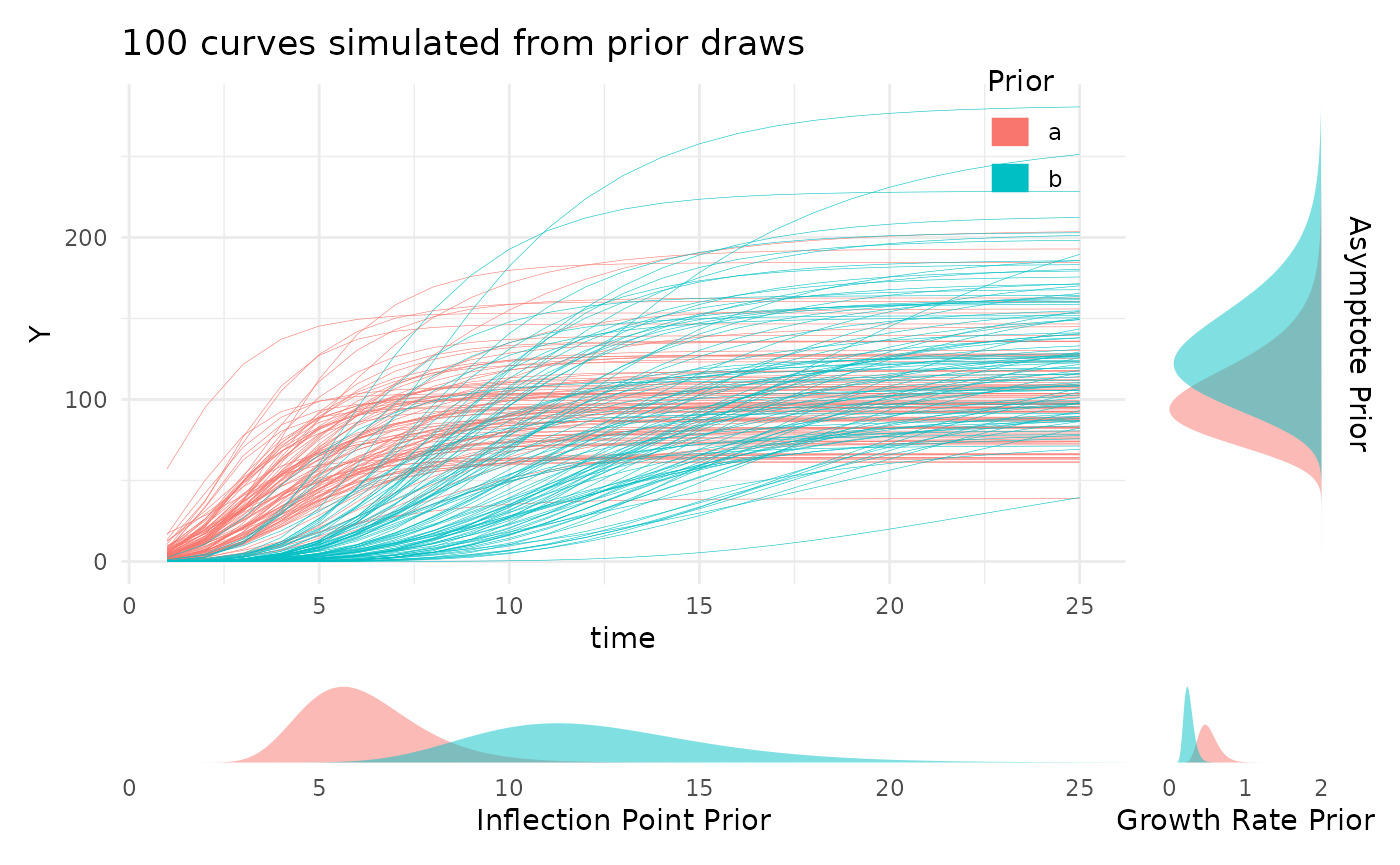

Using growthSS

Now we’re ready to define the necessary variables in our data and use the growthSS function.

sv_ag$group <- interaction(sv_ag$fertilizer, sv_ag$genotype)

The brms package is not always imported by pcvr (since dependencies is NA by default when installing from github), so before fitting models you may need to install that package. For details on installing brms and either rstan or cmdstanr (with cmdstanr being recommended), see those packages linked documentation. Note that if you install pcvr from github with dependencies=T then cmdstanr and brms will be installed and ready to use.

library(brms)
library(cmdstanr)
cmdstanr::install_cmdstan()

Here our priors are informed by a general understanding of what we expect to see for a plant on the bellwether system. In general the example priors

ss <- growthSS(
  model = "gompertz", form = area_cm2 ~ DAS | barcode / group, sigma = "spline", df = sv_ag,
  start = list("A" = 130, "B" = 10, "C" = 0.5), type = "brms"
)

Now we have most of our model components in the ss object. Since we specified a gompertz model we have three parameters, the asymptote (A), the inflection point (B), and the growth rate (C). For other model options see ?pcvr::growthSim for details on the parameters.

Before trying to fit the model it is generally a good idea to check one last plot of the data and make sure you have everything defined correctly.

ggplot(sv_ag, aes(x = DAS, y = area_cm2, group = barcode, color = group)) +
  geom_line() +
  theme_minimal() +
  labs(
    y = expression("Area" ~ "(cm"^2 ~ ")"),
    color = "Genotype\nand Soil"
  )

This looks okay, there are no strange jumps in the data or glaring problems.

Running Models

The fitGrowth function in this case will call brms::brm which automatically uses the output from growthSS. Any additional arguments to brms::brm can still be specified, a few examples of which are shown here.

fit <- fitGrowth(ss,
  iter = 1000, cores = 2, chains = 2, backend = "cmdstanr",
  control = list(adapt_delta = 0.999, max_treedepth = 20)
) # options to increase performance

Check Model Fit

We can visualize credible intervals from a brms model and compare that to our growth trendlines to get an intuitive understanding of how well the model fit. Note that since this vignette does not load brms these are only a picture of the output from brmPlot and brmViolin. The code is present to run this locally if you have brms installed and choose to.

brmPlot(fit, form = area_cm2 ~ DAS | barcode / group, df = ss$df) +
  labs(y = expression("Area" ~ "(cm"^2 ~ ")"))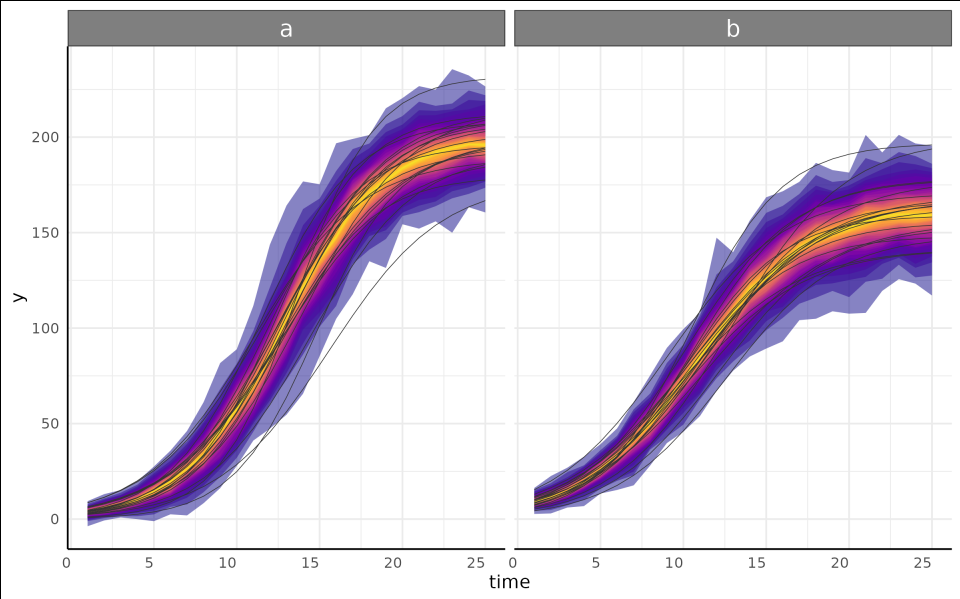

Test Hypotheses

Now we probably have some ideas about what we want to test in our data. The brms::hypothesis function offers incredible flexibility to test all kinds of hypotheses. For consistency with other backends the testGrowth function calls brms::hypothesis to evaluate hypotheses. For some comparisons pcvr has a helper function called brmViolin to visualize posterior distributions and the posterior probability of some hypotheses associated with them.

brmViolin(fit, ss, ".../A_group0.B73 > 1.05") +
  ggplot2::theme(axis.text.x.bottom = ggplot2::element_text(angle = 90))

This shows that we have a posterior probability greater than 99 percent of an asymptotic size at least 5 percent higher with the 100 type soil when compared against the 0 type soil. Note that this data does not have any plants that reached asymptotic size, so the model uses the incomplete data to estimate where an asymptote would be. In a normal experiment the plants would be more mature but here the asymptote parameter is artificially inflated for the 100 soil treatment group due to their slower growth rate.

There are a lot of options for how to use this function and even more ways to use brms::hypothesis, so this example should not be seen as the only way to compare your models.

Multi Value Traits

Working with multi value traits leads to different statistical challenges than the single value traits. Generally reading the data in as wide format makes for a significantly smaller object in memory terms since there are not lots of duplicated metadata (identifiers for each row when every image has hundreds of rows potentially). Note that for many questions even about color it is not necessary to use the entire color histograms. Make sure that you have a good reason to use the complete color data before going down this particular path for too long. As an example, a very simple comparison of the circular mean of Hue here will show our treatment effect in this data.

ggplot(sv_ag[sv_ag$DAS == 18, ], aes(
  x = fertilizer, y = hue_circular_mean_degrees,
  fill = as.character(fertilizer)
)) +
  geom_boxplot(outlier.shape = NA) +
  geom_jitter(width = 0.05, size = 0.5) +
  scale_fill_manual(values = c(viridis::viridis(3, 1, 0.1)), breaks = c("0", "50", "100")) +
  pcv_theme() +
  theme(legend.position = "none") +
  facet_wrap(~genotype, scales = "free_x") +
  scale_x_discrete(limits = c("0", "50", "100")) +
  labs(y = "Hue Circular Mean (degrees)", x = "Soil and Genotype")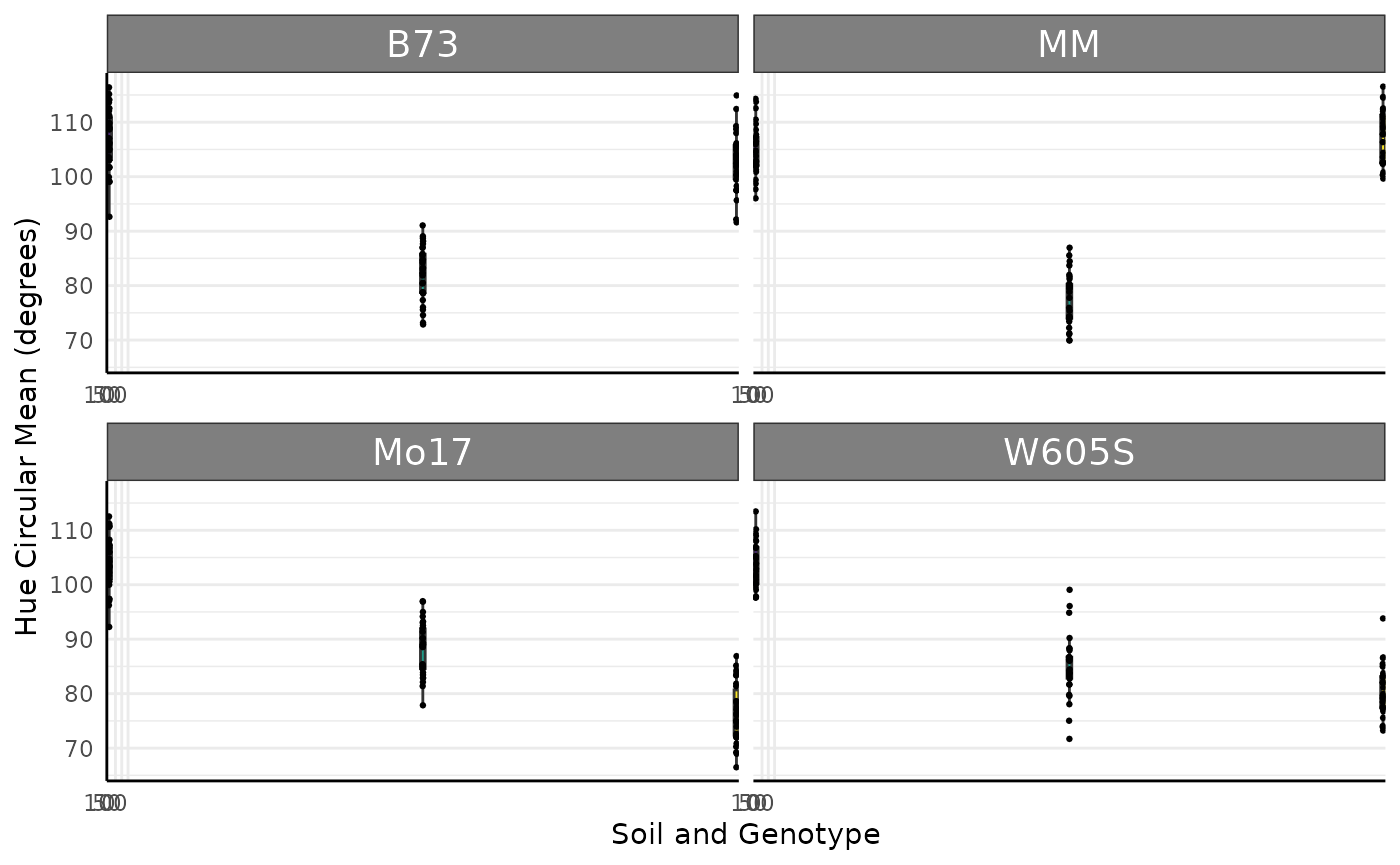

set.seed(123)
dists <- stats::setNames(lapply(runif(12, 50, 60), function(i) {
  list(mean = i, sd = 15)
}), rep("rnorm", 12))
d <- mvSim(dists,
  wide = TRUE, n_samples = 5,
  t = 25, model = "linear",
  params = list("A" = runif(12, 1, 3))
)
d$group <- sapply(sub(".*_", "", d$group), function(x) {
  letters[as.numeric(x)]
})
d$genotype <- ifelse(d$group %in% letters[1:3], "MM",
  ifelse(d$group %in% letters[4:6], "B73",
    ifelse(d$group %in% letters[7:9], "Mo17", "W605S")
  )
)
d$fertilizer <- ifelse(d$group %in% letters[seq(1, 12, 3)], 0,
  ifelse(d$group %in% letters[seq(2, 12, 3)], 50, 100)
)
colnames(d)[1] <- "DAS"
colnames(d) <- gsub("sim_", "hue_frequencies_", colnames(d))
hue_wide <- d

Joyplots

Joyplots are a common way to look at lots of distributions. Here we check the hue histograms as joyplots using three days and add a new fill for the hue colorspace. Joyplots can be made with long or wide multi-value traits.

p <- pcv.joyplot(hue_wide[hue_wide$DAS %in% c(5, 10, 15), ],
  index = "hue_frequencies", group = c("fertilizer", "genotype"),
  y = "DAS", id = NULL
)
p + scale_fill_gradientn(colors = scales::hue_pal(l = 65)(360)) +
  scale_y_discrete(limits = c("5", "10", "15"))

As mentioned previously the conjugate function can be used with wide multi-value data. To use multi value data the samples should be data frames or matrices representing color histograms. Here we compare our color histograms assuming a lognormal distribution and find that they are very similar in this parameterization.

mo17_sample <- hue_wide[
  hue_wide$genotype == "Mo17" & hue_wide$DAS > 18 & hue_wide$fertilizer == 100,
  grepl("hue_freq", colnames(hue_wide))
]
b73_sample <- hue_wide[
  hue_wide$genotype == "B73" & hue_wide$DAS > 18 & hue_wide$fertilizer == 100,
  grepl("hue_freq", colnames(hue_wide))
]

hue_res_ln <- conjugate(
  s1 = mo17_sample, s2 = b73_sample, method = "lognormal",
  plot = TRUE, rope_range = c(-10, 10), hypothesis = "equal"
)

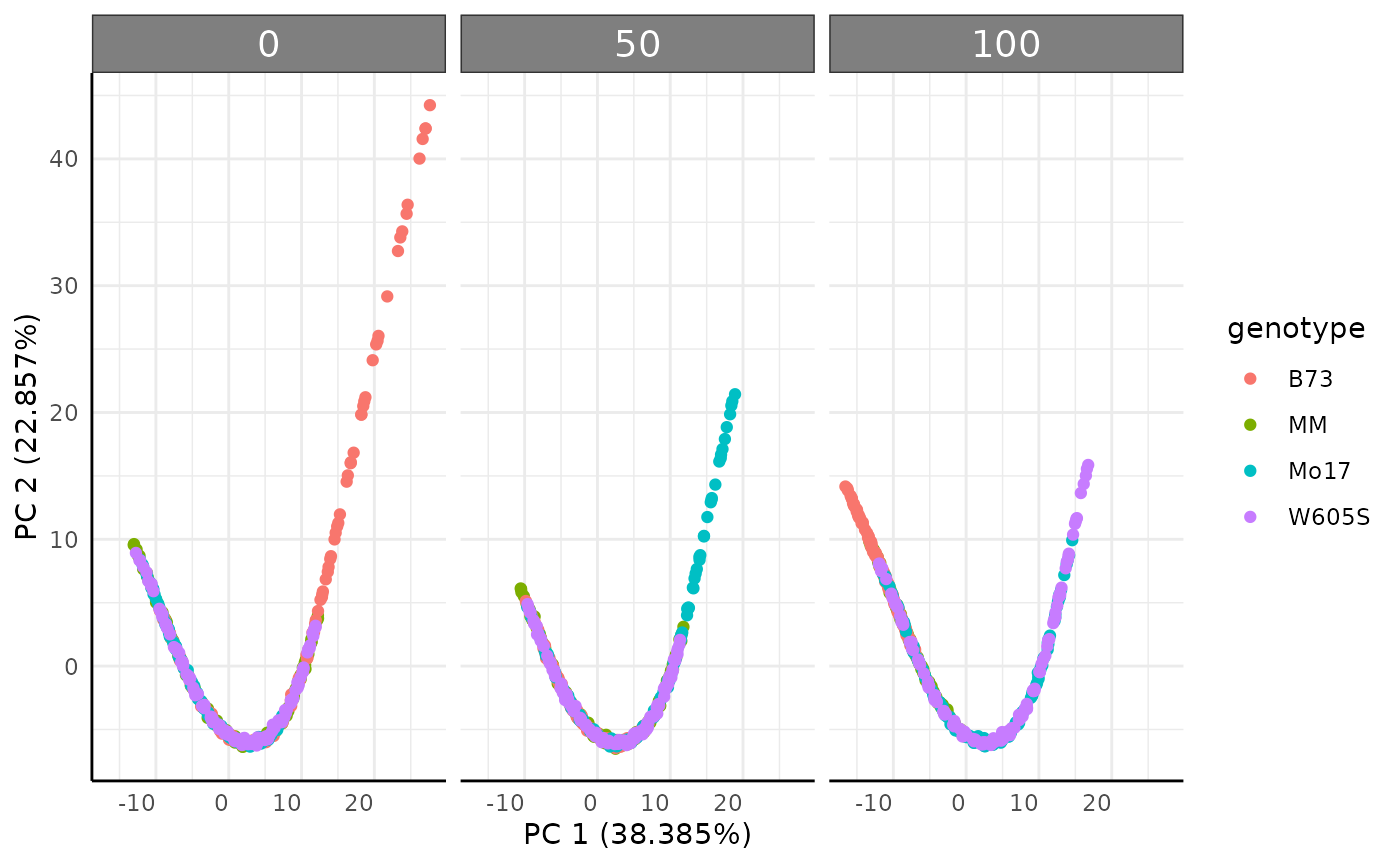
Ordination

Ordinations are another common way to look at multi value traits. The pcadf function runs ordinations and optionally returns the PCs with metadata. Here our simulated data does has a very deterministic pattern due.

pcadf(hue_wide, cols = "hue_frequencies", color = "genotype", returnData = FALSE) +
  facet_wrap(~ factor(fertilizer, levels = c("0", "50", "100")))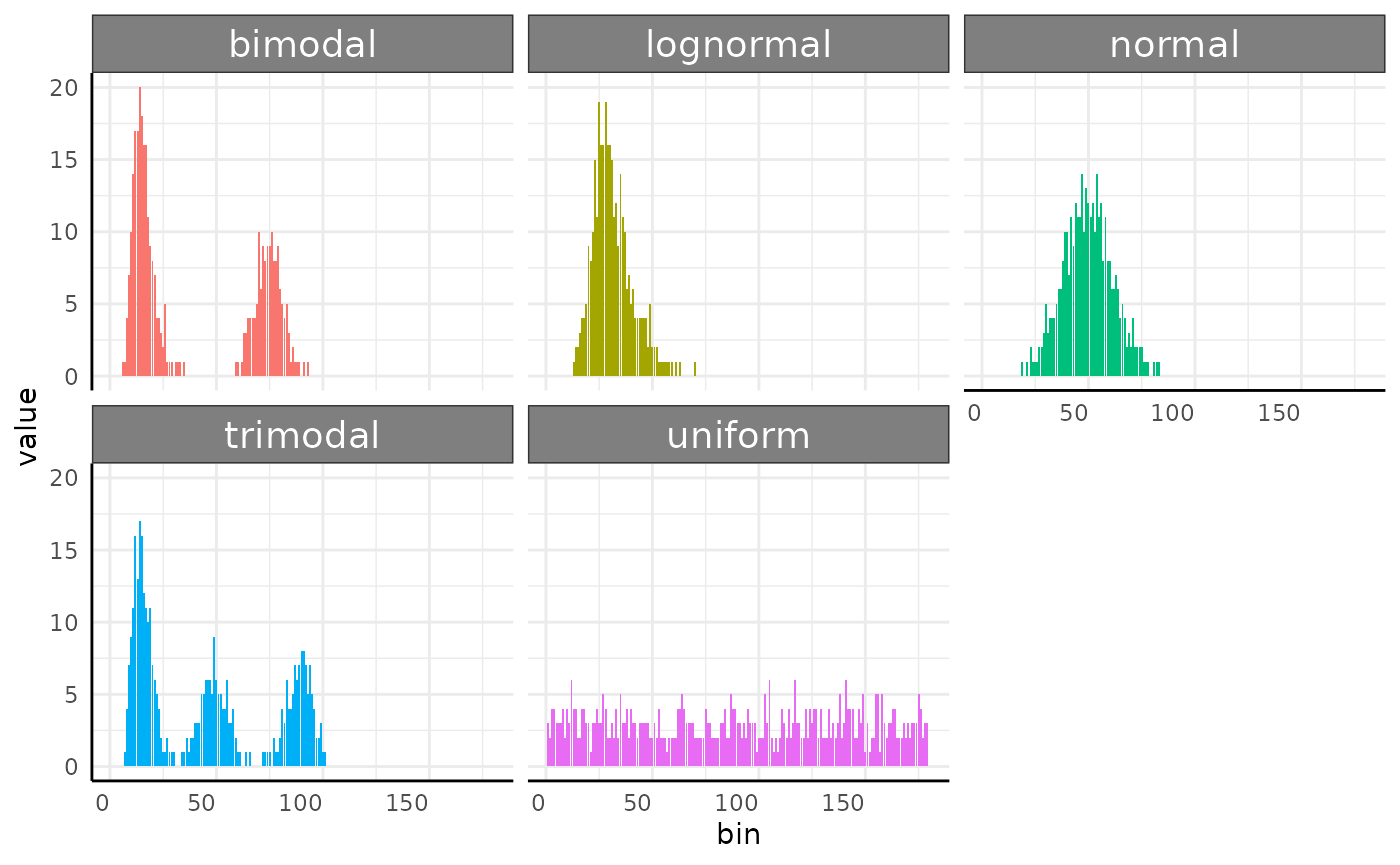

Earth Mover’s Distance

Since color data is exported from plantCV as histogram data we can also use Earth Mover’s Distance (EMD) to compare images. Conceptually EMD is a distance that quantifies how much work it would take to turn one histogram into another. Here we do pairwise comparisons of all our rows and return a long dataframe of those distances. Note that even running several cores in parallel this can take a lot of time for larger datasets since the number of comparisons quickly can become unwieldy. The output also will require more work to keep analyzing, so make sure this is what you want to be doing before using EMD to compare color histograms. If you are only interested in a change of the mean then this is probably not the best way to use your data.

Here is a fast example of a place where EMD makes a lot of sense. In this simulated data we have five generating distributions. Normal, Log Normal, Bimodal, Trimodal, and Uniform. We could use some gaussian mixtures to characterize the multi-modal histograms but that will get clunky for comparing to the unimodal or uniform distributions. The conjugate function would not work here since these distributions do not share a common parameterization. Instead, we can use EMD.

set.seed(123)

simFreqs <- function(vec, group) {
  s1 <- hist(vec, breaks = seq(1, 181, 1), plot = FALSE)$counts
  s1d <- as.data.frame(cbind(data.frame(group), matrix(s1, nrow = 1)))
  colnames(s1d) <- c("group", paste0("sim_", 1:180))
  s1d
}

sim_df <- rbind(
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(rnorm(200, 50, 10), group = "normal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(rlnorm(200, log(30), 0.25), group = "lognormal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(c(rlnorm(125, log(15), 0.25), rnorm(75, 75, 5)), group = "bimodal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(c(rlnorm(100, log(15), 0.25), rnorm(50, 50, 5), rnorm(50, 90, 5)), group = "trimodal")
  })),
  do.call(rbind, lapply(1:10, function(i) {
    simFreqs(runif(200, 1, 180), group = "uniform")
  }))
)

sim_df_long <- as.data.frame(data.table::melt(data.table::as.data.table(sim_df), id.vars = "group"))
sim_df_long$bin <- as.numeric(sub("sim_", "", sim_df_long$variable))

ggplot(sim_df_long, aes(x = bin, y = value, fill = group), alpha = 0.25) +
  geom_col(position = "identity", show.legend = FALSE) +
  pcv_theme() +
  facet_wrap(~group)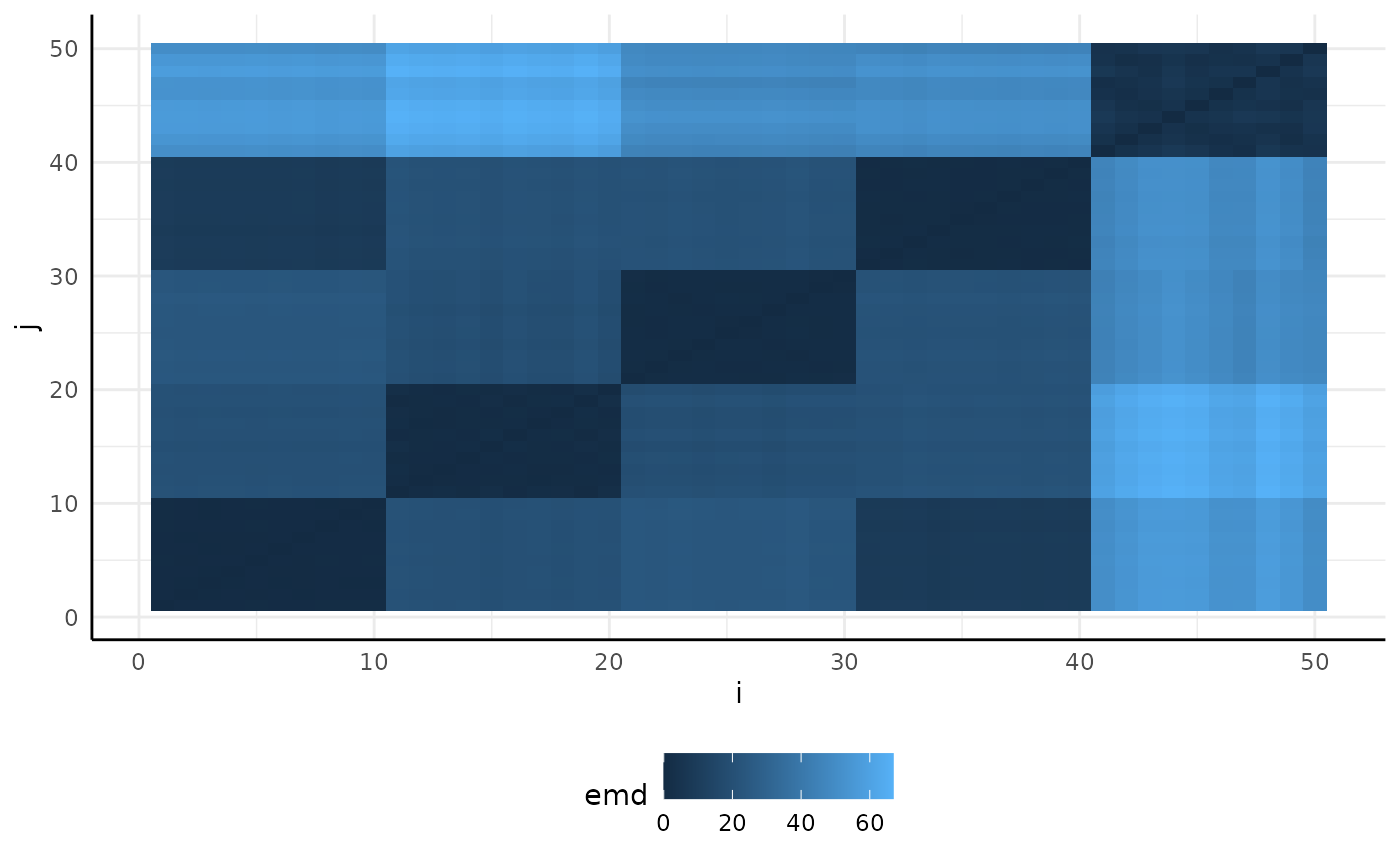

Our plots show very different distributions, so we get EMD between our images and see that we do have some trends shown in the resulting heatmap.

sim_emd <- pcv.emd(
  df = sim_df, cols = "sim_", reorder = c("group"),
  mat = FALSE, plot = TRUE, parallel = 1, raiseError = TRUE
)

## Estimated time of calculation is roughly 3.1 seconds using 1 cores in parallel.

sim_emd$plot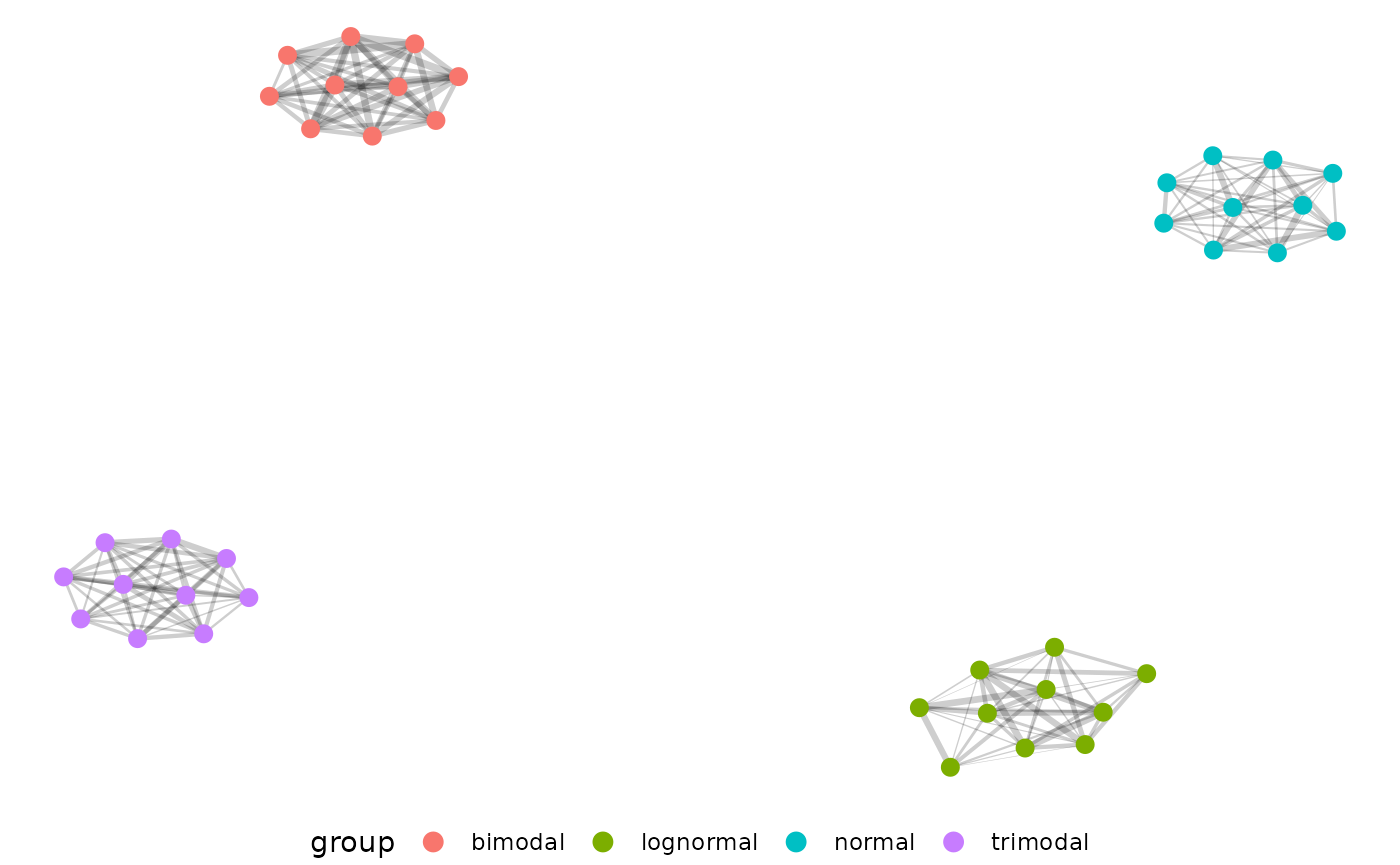

Now we can filter edge strength during our network building step for EMD > 0.5, and plot our network.

n <- pcv.net(sim_emd$data, filter = 0.5)
net.plot(n, fill = "group")

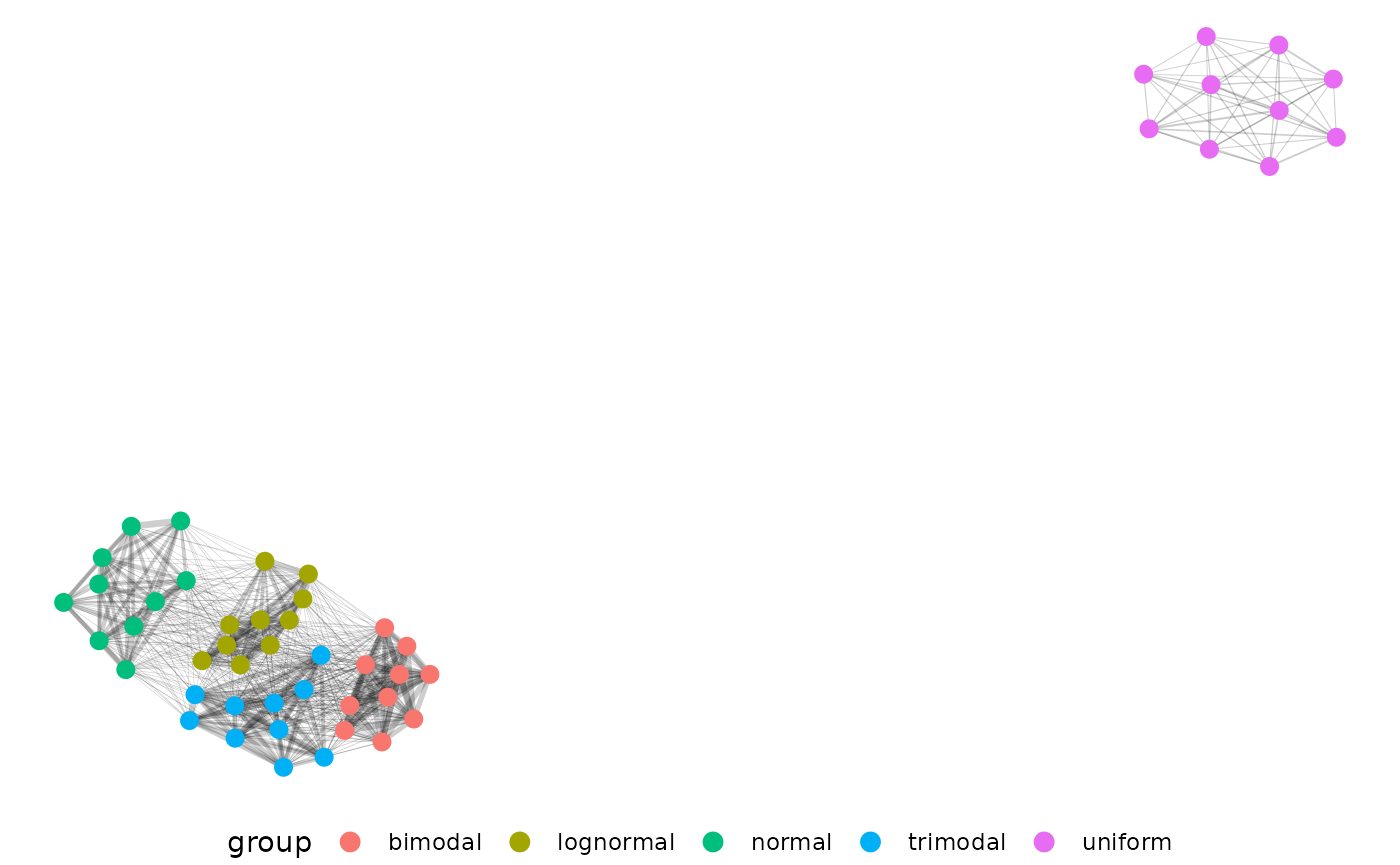
The distributions separate very well from each other, but we don’t actually see our uniform distribution here. That is because the uniform distribution does not have self-similar replicates and is also not very similar to the other distributions. If we change our filtering then we can even see which generating distributions are most similar to each other. Here we pass 0.5 as a string, which tells pcv.net to use the top 50 percent of EMD values instead of EMD values > 0.5.

n <- pcv.net(sim_emd$data, filter = "0.5")
net.plot(n, fill = "group")

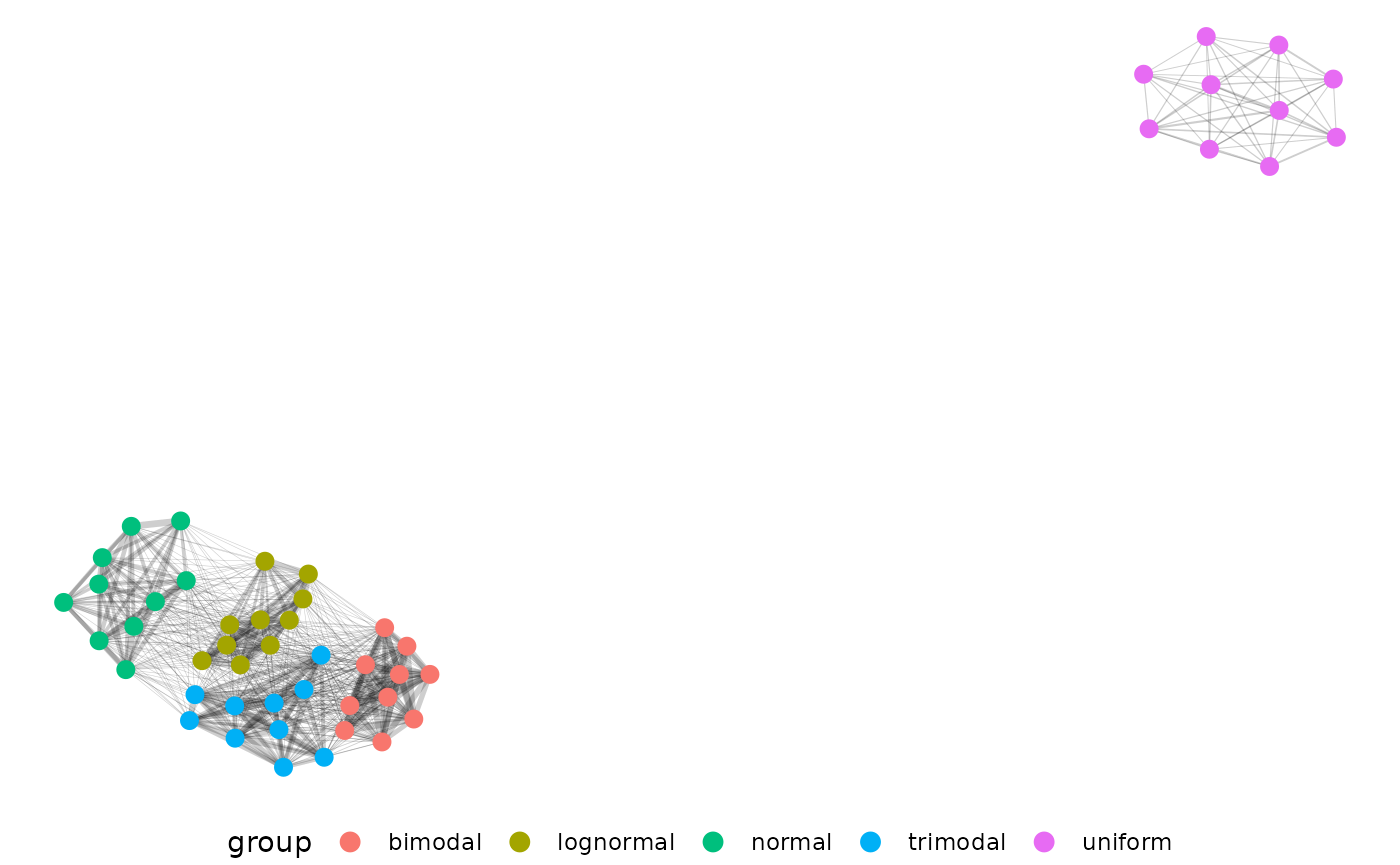
Just as we’d expect, our uniform distribution shows up now and is the most different. Now changing the edgeFilter in the net.plot function would let us fine tune this plot more to show finer distinctions between our other four generating distributions.

Here is an example of how we might use hue data.

EMD <- pcv.emd(
  df = hue_wide[hue_wide$DAS %in% c(5, 12, 19), ], cols = "hue_frequencies",
  reorder = c("fertilizer", "genotype", "DAS"),
  mat = FALSE, plot = TRUE, parallel = 12, raiseError = TRUE
)

EMD can get very heavy with large datasets. For a recent lemnatech dataset using only the images from every 5th day there were $6332^2$ = 40,094,224 pairwise EMD values. In long format that’s a 40 million row dataframe, which is unwieldy. To get around this problem we might decide to use the hue circular mean as a single value trait or to aggregate some of our data with the mv_ag function.

Starting with our complete hue data we have 1500 image histograms. The mv_ag function will take a group argument and randomly pick members of that group to have their histograms combined. Note that histograms are scaled to sum to 1 before they are sampled. Here we return one example with 2 histograms kept per group and one example where groups are summarized into 1 histogram. If there are equal or fewer images as the n_per_group argument then no aggregation is done for that group but data are rescaled.

hue_ag1 <- mv_ag(df = hue_wide, group = c("DAS", "genotype", "fertilizer"), n_per_group = 2)
dim(hue_ag1)

## [1] 600 183

hue_ag2 <- mv_ag(hue_wide, group = c("DAS", "genotype", "fertilizer"), n_per_group = 1)
dim(hue_ag2)

## [1] 300 183

Network Analysis

As it stands our EMD data is potentially difficult to use for those unfamiliar with distance matrix based analysis. Here we represent our distances as a network to help use the results.

set.seed(456)
net <- pcv.net(EMD$data, meta = c("fertilizer", "genotype", "DAS"), filter = 0.5)

net.plot(net, fill = "DAS", shape = "fertilizer", size = 2)

Our example network shows some clustering but real data’s patterns are likely to be more complex:

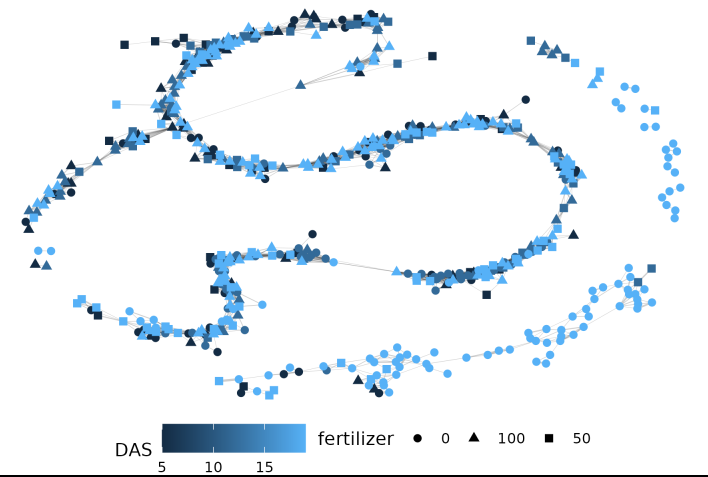
This is a much more complicated network! Parsing biological meaning out of this would require more work than the first example with 5 very different distributions, but there is a pretty strong cluster in the upper right corner of plants with low fertilizer at the end of the experiment. In general if you pick to use EMD with or without networks start small and consider what each step should mean conceptually for your experiment.

Conclusion

This vignette will be periodically updated as pcvr changes. Generally the tutorials are updated more frequently and can be a good resource. Once again if your goal or experiment has some set of questions or needs that are not met so far please consider making an issue on github to help the Data Science Core continue to work on this project in ways that will help the plantCV community.